Nested lists

A nested list is a list that appears as an element in another list. In this list, the element with index 3 is a nested list:

>>> nested = ["hello", 2.0, 5, [10, 20]]

If we output the element at index 3, we get:

>>> print(nested[3])
[10, 20]

To extract an element from the nested list, we can proceed in two steps:

>>> elem = nested[3]
>>> elem[0]
10

Or we can combine them:

>>> nested[3][1]
20

Bracket operators evaluate from left to right, so this expression gets the 3'th element of nested and extracts the 1'th element from it.

Matrices

Nested lists are often used to represent matrices. For example, consider this matrix:

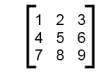>>> mx = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

mx is a list with three elements, where each element is a row of the matrix. We can select an entire row from the matrix in the usual way:

>>> mx[1]
[4, 5, 6]

Or we can extract a single element from the matrix using the double-index form:

>>> mx[1][2]
6

The first index selects the row, and the second index selects the column. Although this way of representing matrices is common, it is not the only possibility. A small variation is to use a list of columns instead of a list of rows. Later we will see a more radical alternative using a dictionary.

An interesting question is how we can create a matrix of arbitrary size in a practical manner. Many solutions are possible, some of which are more readable than others. This is full code that creates a matrix using the append method:

def matrix(n):
  """ Returns an n times n matrix with zeros, represented using lists
  within lists """
  m = []
  for j in range(n):
    l = []
    for i in range(n):
      l.append ( 0 )
    m.append ( l )
  return m

In this code, m is the matrix we are going to return. Within this list, we are creating n nested lists. Each of these nested lists is a list of n 0s.

It could be tempting to write this code instead:

def matrix_incorrect(n):
  l = []
  for i in range(n):
    l.append ( 0 )
  m = []
  for j in range(n):
    m.append ( l )
  return m

At first sight, it may seem that this code is correct. If you execute print(matrix_incorrect(3)) you will indeed see this output:

[[0, 0, 0], [0, 0, 0], [0, 0, 0]]

However, the data structure created by this function has undesirable properties. If we execute the following code:

m = matrix_incorrect(3)
m[0][0] = 1
print(m)

we will see the following output:

[[1, 0, 0], [1, 0, 0], [1, 0, 0]]

This is most likely not the output that you were looking for; indeed, any modification of one row, will also lead to a modification of the other rows.

The explanation for this can be found in how Python deals with objects and references. The append method takes as argument a reference to an object, and will add a reference to this object to the list. In our code, we have first created a list for which l is a reference. Subsequently, we add this reference three times to the list m. As a result, all three elements in the list m point towards the same underlying list. As m[0], m[1], m[2] all point towards the same list, any change to m[0] will also be visible when printing m[1] and m[2].

Our original code did not have this problem, as we created a new nested list n times.

The following code would avoid this problem:

def matrix_incorrect(n):
  l = []
  for i in range(n):
    l.append ( 0 )
  m = []
  for j in range(n):
    m.append ( list(l) )
  return m

The main difference is here that we use the list(l) construction. This construction will first create a copy of l: it will create a new list object that contains the same elements as l; the reference to this new object is added t the list m. As we create n copies of the original list l, all these nested lists are now independent of each other.

Glossary

nested list

A list that is an element of another list.

References