Table des matières
Data Structures
Strings
Source: this section is heavily based on Chapter 8 of [ThinkCS].
A compound data type
So far we have seen built-in types like int, float, bool, str and we've seen lists and pairs. Strings, lists, and pairs are qualitatively different from the others because they are made up of smaller pieces. In the case of strings, they're made up of smaller strings each containing one character.
Types that comprise smaller pieces are called compound data types. Depending on what we are doing, we may want to treat a compound data type as a single thing, or we may want to access its parts. This ambiguity is useful.
Working with strings as single things
We previously saw that each turtle instance has its own attributes and a number of methods that can be applied to the instance. For example, we could set the turtle's color, and we wrote tess.turn(90).
Just like a turtle, a string is also an object. So each string instance has its own attributes and methods.
For example:
>>> ss = "Hello, World!" >>> tt = ss.upper() >>> tt 'HELLO, WORLD!'
upper is a method that can be invoked on any string object to create a new string, in which all the characters are in uppercase. (The original string ss remains unchanged.)
There are also methods such as lower, capitalize, and swapcase that do other interesting stuff. A complete list of the functions that can be called on a string can be found online: https://docs.python.org/3/library/stdtypes.html#string-methods. This webpage is part of the online documentation of Python, and provides a complete overview of all functionality supported by strings. You are not required to know these functions by heart; it is only important that you understand that strings are objects on which methods can be applied, and that there is a documentation that explains the different methods that can be applied on strings.
Working with the parts of a string
The indexing operator (Python uses square brackets to enclose the index) selects a single character substring from a string:
>>> fruit = "banana" >>> m = fruit[1] >>> print(m)
The expression fruit[1] selects character number 1 from fruit, and creates a new string containing just this one character. The variable m refers to the result. When we display m, we could get a surprise:
a
Computer scientists always start counting from zero! The letter at subscript position zero of "banana" is b. So at position [1] we have the letter a.
If we want to access the zero-eth letter of a string, we just place 0, or any expression that evaluates to 0, in between the brackets:
>>> m = fruit[0] >>> print(m) b
The expression in brackets is called an index. An index specifies a member of an ordered collection, in this case the collection of characters in the string. The index indicates which one you want, hence the name. It can be any integer expression.
Note that the result of fruit[0] is a string itself. As a result, we can do anything on fruit[0] that can be done on strings, such as fruit[0].upper () to obtain a capitalized version of this letter.
We can use enumerate to visualize the indices that can be used to access a string:
>>> fruit = "banana" >>> list(enumerate(fruit)) [(0, 'b'), (1, 'a'), (2, 'n'), (3, 'a'), (4, 'n'), (5, 'a')]
Do not worry about enumerate at this point, we will see more of it in the chapter on lists.
Note that indexing returns a string --- Python has no special type for a single character. It is just a string of length 1.
We've also seen lists previously. The same indexing notation works to extract elements from a list:
>>> prime_nums = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] >>> prime_nums[4] 11 >>> friends = ["Joe", "Zoe", "Brad", "Angelina", "Zuki", "Thandi", "Paris"] >>> friends[3] 'Angelina'
Length
The len function, when applied to a string, returns the number of characters in a string:
>>> fruit = "banana" >>> len(fruit) 6
To get the last letter of a string, you might be tempted to try something like this:
sz = len(fruit) last = fruit[sz] # ERROR!
That won't work. It causes the runtime error IndexError: string index out of range. The reason is that there is no character at index position 6 in "banana". Because we start counting at zero, the six indexes are numbered 0 to 5. To get the last character, we have to subtract 1 from the length of fruit:
sz = len(fruit) last = fruit[sz-1]
Alternatively, we can use negative indices, which count backward from the end of the string. The expression fruit[-1] yields the last letter, fruit[-2] yields the second to last, and so on.
As you might have guessed, indexing with a negative index also works like this for lists.
We won't use negative indexes in the rest of these notes --- not many computer languages use this idiom, and you'll probably be better off avoiding it. But there is plenty of Python code out on the Internet that will use this trick, so it is best to know that it exists.
Traversal and the for loop
A lot of computations involve processing a string one character at a time. Often they start at the beginning, select each character in turn, do something to it, and continue until the end. This pattern of processing is called a traversal. One way to encode a traversal is with a while statement:
ix = 0 while ix < len(fruit): letter = fruit[ix] print(letter) ix += 1
This loop traverses the string and displays each letter on a line by itself. The loop condition is ix < len(fruit), so when ix is equal to the length of the string, the condition is false, and the body of the loop is not executed. The last character accessed is the one with the index len(fruit)-1, which is the last character in the string.
But we've previously seen how the for loop can easily iterate over the elements in a list and it can do so for strings as well:
for c in fruit: print(c)
Each time through the loop, the next character in the string is assigned to the variable c. The loop continues until no characters are left. Here we can see the expressive power the for loop gives us compared to the while loop when traversing a string.
The following example shows how to use concatenation and a for loop to generate an abecedarian series. Abecedarian refers to a series or list in which the elements appear in alphabetical order. For example, in Robert McCloskey's book Make Way for Ducklings, the names of the ducklings are Jack, Kack, Lack, Mack, Nack, Ouack, Pack, and Quack. This loop outputs these names in order:
prefixes = "JKLMNOPQ" suffix = "ack" for p in prefixes: print(p + suffix)
The output of this program is:
Jack Kack Lack Mack Nack Oack Pack Qack
Of course, that's not quite right because Ouack and Quack are misspelled. You'll fix this as an exercise below.
Slices
A substring of a string is obtained by taking a slice. Similarly, we can slice a list to refer to some sublist of the items in the list:
>>> s = "Pirates of the Caribbean" >>> print(s[0:7]) Pirates >>> print(s[11:14]) the >>> print(s[15:24]) Caribbean >>> friends = ["Joe", "Zoe", "Brad", "Angelina", "Zuki", "Thandi", "Paris"] >>> print(friends[2:4]) ['Brad', 'Angelina']
The operator [n:m] returns the part of the string from the n'th character to the m'th character, including the first but excluding the last. This behavior makes sense if you imagine the indices pointing between the characters, as in the following diagram:
If you imagine this as a piece of paper, the slice operator [n:m] copies out the part of the paper between the n and m positions. Provided m and n are both within the bounds of the string, your result will be of length (m-n).
Three tricks are added to this: if you omit the first index (before the colon), the slice starts at the beginning of the string (or list). If you omit the second index, the slice extends to the end of the string (or list). Similarly, if you provide value for n that is bigger than the length of the string (or list), the slice will take all the values up to the end. (It won't give an "out of range" error like the normal indexing operation does.) Thus:
>>> fruit = "banana" >>> fruit[:3] 'ban' >>> fruit[3:] 'ana' >>> fruit[3:999] 'ana'
What do you think s[:] means? What about friends[4:]?
String comparison
The comparison operators work on strings. To see if two strings are equal:
if word == "banana": print("Yes, we have no bananas!")
Other comparison operations are useful for putting words in lexicographical order:
if word < "banana": print("Your word, " + word + ", comes before banana.") elif word > "banana": print("Your word, " + word + ", comes after banana.") else: print("Yes, we have no bananas!")
This is similar to the alphabetical order you would use with a dictionary, except that all the uppercase letters come before all the lowercase letters. As a result:
Your word, Zebra, comes before banana.
A common way to address this problem is to convert strings to a standard format, such as all lowercase, before performing the comparison. A more difficult problem is making the program realize that zebras are not fruit.
Strings are immutable
It is tempting to use the [] operator on the left side of an assignment, with the intention of changing a character in a string. For example:
greeting = "Hello, world!" greeting[0] = 'J' # ERROR! print(greeting)
Instead of producing the output Jello, world!, this code produces the runtime error TypeError: 'str' object does not support item assignment.
Strings are immutable, which means you can't change an existing string. The best you can do is create a new string that is a variation on the original:
greeting = "Hello, world!" new_greeting = "J" + greeting[1:] print(new_greeting)
The solution here is to concatenate a new first letter onto a slice of greeting. This operation has no effect on the original string.
A find function
What does the following function do?
def find(strng, ch): """ Find and return the index of ch in strng. Return -1 if ch does not occur in strng. """ ix = 0 while ix < len(strng): if strng[ix] == ch: return ix ix += 1 return -1 test(find("Compsci", "p") == 3) test(find("Compsci", "C") == 0) test(find("Compsci", "i") == 6) test(find("Compsci", "x") == -1)
In a sense, find is the opposite of the indexing operator. Instead of taking an index and extracting the corresponding character, it takes a character and finds the index where that character appears. If the character is not found, the function returns -1.
This is another example where we see a return statement inside a loop. If strng[ix] == ch, the function returns immediately, breaking out of the loop prematurely.
If the character doesn't appear in the string, then the program exits the loop normally and returns -1.
This pattern of computation is sometimes called a eureka traversal or short-circuit evaluation, because as soon as we find what we are looking for, we can cry "Eureka!", take the short-circuit, and stop looking.
Looping and counting
The following program counts the number of times the letter a appears in a string, and is another example of the counter pattern introduced in counting:
def count_a(text): count = 0 for c in text: if c == "a": count += 1 return(count) test(count_a("banana") == 3)
Optional parameters (Optional topic)
Python offers powerful features that make programming easier for experienced programmers. One such feature are optional parameters. You are encouraged to read about them; many Python programmers often use optional parameters. However, if you are just starting as a programmer, you are free to skip this section; this topic is not mandatory within this course.
To understand why optional parameters are useful, consider the following example. Suppose we want to find the first occurrence of a character in a string, considering only locations in the string starting from a given location. We can modify the find function, adding a third parameter for the starting position in the search string:
def find2(strng, ch, start): ix = start while ix < len(strng): if strng[ix] == ch: return ix ix += 1 return -1 test(find2("banana", "a", 2) == 3)
The call find2("banana", "a", 2) now returns 3, the index of the first occurrence of "a" in "banana" starting the search at index 2. What does find2("banana", "n", 3) return? If you said 3, there is a good chance you understand how find2 works.
Better still, we can combine find and find2 using an optional parameter:
def find(strng, ch, start=0): ix = start while ix < len(strng): if strng[ix] == ch: return ix ix += 1 return -1
When a function has an optional parameter, the caller may provide a matching argument. If the third argument is provided to find, it gets assigned to start. But if the caller leaves the argument out, then start is given a default value indicated by the assignment start=0 in the function definition.
So the call find("banana", "a", 2) to this version of find behaves just like find2, while in the call find("banana", "a"), start will be set to the default value of 0.
Adding another optional parameter to find makes it search from a starting position, up to but not including the end position:
def find(strng, ch, start=0, end=None): ix = start if end is None: end = len(strng) while ix < end: if strng[ix] == ch: return ix ix += 1 return -1
The optional value for end is interesting: we give it a default value None if the caller does not supply any argument. In the body of the function we test what end is, and if the caller did not supply any argument, we reassign end to be the length of the string. If the caller has supplied an argument for end, however, the caller's value will be used in the loop.
The semantics of start and end in this function are precisely the same as they are in the range function.
Here are some test cases that should pass:
ss = "Python strings have some interesting methods." test(find(ss, "s") == 7) test(find(ss, "s", 7) == 7) test(find(ss, "s", 8) == 13) test(find(ss, "s", 8, 13) == -1) test(find(ss, ".") == len(ss)-1)
The in and not in operators (Optional topic)
The in operator tests for membership. When both of the arguments to in are strings, in checks whether the left argument is a substring of the right argument.
>>> "p" in "apple" True >>> "i" in "apple" False >>> "ap" in "apple" True >>> "pa" in "apple" False
Note that a string is a substring of itself, and the empty string is a substring of any other string. (Also note that computer scientists like to think about these edge cases quite carefully!)
>>> "a" in "a" True >>> "apple" in "apple" True >>> "" in "a" True >>> "" in "apple" True
The not in operator returns the logical opposite results of in:
>>> "x" not in "apple" True
Combining the in operator with string concatenation using +, we can write a function that removes all the vowels from a string:
def remove_vowels(s): vowels = "aeiouAEIOU" s_sans_vowels = "" for x in s: if x not in vowels: s_sans_vowels += x return s_sans_vowels test(remove_vowels("compsci") == "cmpsc") test(remove_vowels("aAbEefIijOopUus") == "bfjps")
The built-in find method (Optional topic)
Now that we've done all this work to write a powerful find function, we can reveal that strings already have their own built-in find method. It can do everything that our code can do, and more!
test(ss.find("s") == 7) test(ss.find("s", 7) == 7) test(ss.find("s", 8) == 13) test(ss.find("s", 8, 13) == -1) test(ss.find(".") == len(ss)-1)
The built-in find method is more general than our version. It can find substrings, not just single characters:
>>> "banana".find("nan") 2 >>> "banana".find("na", 3) 4
Usually we'd prefer to use the methods that Python provides rather than reinvent our own equivalents. But many of the built-in functions and methods make good teaching exercises, and the underlying techniques you learn are your building blocks to becoming a proficient programmer.
The split method (Optional topic)
One of the most useful methods on strings is the split method: it splits a single multi-word string into a list of individual words, removing all the whitespace between them. (Whitespace means any tabs, newlines, or spaces.) This allows us to read input as a single string, and split it into words.
>>> ss = "Well I never did said Alice" >>> wds = ss.split() >>> wds ['Well', 'I', 'never', 'did', 'said', 'Alice']
Cleaning up your strings (Optional topic)
We'll often work with strings that contain punctuation, or tab and newline characters, especially, as we'll see in a future chapter, when we read our text from files or from the Internet. But if we're writing a program, say, to count word frequencies or check the spelling of each word, we'd prefer to strip off these unwanted characters.
We'll show just one example of how to strip punctuation from a string. Remember that strings are immutable, so we cannot change the string with the punctuation --- we need to traverse the original string and create a new string, omitting any punctuation:
punctuation = "!\"#$%&'()*+,-./:;<=>?@[\\]^_`{|}~" def remove_punctuation(s): s_sans_punct = "" for letter in s: if letter not in punctuation: s_sans_punct += letter return s_sans_punct
Setting up that first assignment is messy and error-prone. Fortunately, the Python string module already does it for us. So we will make a slight improvement to this program --- we'll import the string module and use its definition:
import string def remove_punctuation(s): s_without_punct = "" for letter in s: if letter not in string.punctuation: s_without_punct += letter return s_without_punct test(remove_punctuation('"Well, I never did!", said Alice.') == "Well I never did said Alice") test(remove_punctuation("Are you very, very, sure?") == "Are you very very sure")
Composing together this function and the split method from the previous section makes a useful combination --- we'll clean out the punctuation, and split will clean out the newlines and tabs while turning the string into a list of words:
my_story = """ Pythons are constrictors, which means that they will 'squeeze' the life out of their prey. They coil themselves around their prey and with each breath the creature takes the snake will squeeze a little tighter until they stop breathing completely. Once the heart stops the prey is swallowed whole. The entire animal is digested in the snake's stomach except for fur or feathers. What do you think happens to the fur, feathers, beaks, and eggshells? The 'extra stuff' gets passed out as --- you guessed it --- snake POOP! """ wds = remove_punctuation(my_story).split() print(wds)
The output:
['Pythons', 'are', 'constrictors', ... , 'it', 'snake', 'POOP']
As indicated earlier, there are other useful string methods, but this book isn't intended to be a reference manual. You can find all necessary information in the Python Library Reference online.
The string format method (Optional topic)
The easiest and most powerful way to format a string in Python 3 is to use the format method. To see how this works, let's start with a few examples:
s1 = "His name is {0}!".format("Arthur") print(s1) name = "Alice" age = 10 s2 = "I am {1} and I am {0} years old.".format(age, name) print(s2) n1 = 4 n2 = 5 s3 = "2**10 = {0} and {1} * {2} = {3:f}".format(2**10, n1, n2, n1 * n2) print(s3)
Running the script produces:
His name is Arthur! I am Alice and I am 10 years old. 2**10 = 1024 and 4 * 5 = 20.000000
The template string contains place holders, ... {0} ... {1} ... {2} ... etc. The format method substitutes its arguments into the place holders. The numbers in the place holders are indexes that determine which argument gets substituted --- make sure you understand line 6 above!
But there's more! Each of the replacement fields can also contain a format specification --- it is always introduced by the : symbol (Line 11 above uses one.) This modifies how the substitutions are made into the template, and can control things like:
- whether the field is aligned to the left <, center ^, or right >
- the width allocated to the field within the result string (a number like 10)
- the type of conversion (we'll initially only force conversion to float, f, as we did in line 11 of the code above, or perhaps we'll ask integer numbers to be converted to hexadecimal using x)
- if the type conversion is a float, you can also specify how many decimal places are wanted (typically, .2f is useful for working with currencies to two decimal places.)
Let's do a few simple and common examples that should be enough for most needs. If you need to do anything more esoteric, use help and read all the powerful, gory details.
n1 = "Paris" n2 = "Whitney" n3 = "Hilton" print("Pi to three decimal places is {0:.3f}".format(3.1415926)) print("123456789 123456789 123456789 123456789 123456789 123456789") print("|||{0:<15}|||{1:^15}|||{2:>15}|||Born in {3}|||" .format(n1,n2,n3,1981)) print("The decimal value {0} converts to hex value {0:x}" .format(123456))
This script produces the output:
Pi to three decimal places is 3.142 123456789 123456789 123456789 123456789 123456789 123456789 |||Paris ||| Whitney ||| Hilton|||Born in 1981||| The decimal value 123456 converts to hex value 1e240
You can have multiple placeholders indexing the same argument, or perhaps even have extra arguments that are not referenced at all:
letter = """ Dear {0} {2}. {0}, I have an interesting money-making proposition for you! If you deposit $10 million into my bank account, I can double your money ... """ print(letter.format("Paris", "Whitney", "Hilton")) print(letter.format("Bill", "Henry", "Gates"))
This produces the following:
Dear Paris Hilton. Paris, I have an interesting money-making proposition for you! If you deposit $10 million into my bank account, I can double your money ... Dear Bill Gates. Bill, I have an interesting money-making proposition for you! If you deposit $10 million into my bank account I can double your money ...
As you might expect, you'll get an index error if your placeholders refer to arguments that you do not provide:
>>> "hello {3}".format("Dave") Traceback (most recent call last): File "<interactive input>", line 1, in <module> IndexError: tuple index out of range
The following example illustrates the real utility of string formatting. First, we'll try to print a table without using string formatting:
print("i\ti**2\ti**3\ti**5\ti**10\ti**20") for i in range(1, 11): print(i, "\t", i**2, "\t", i**3, "\t", i**5, "\t", i**10, "\t", i**20)
This program prints out a table of various powers of the numbers from 1 to 10. (This assumes that the tab width is 8. You might see something even worse than this if you tab width is set to 4.) In its current form it relies on the tab character ( \t) to align the columns of values, but this breaks down when the values in the table get larger than the tab width:
i i**2 i**3 i**5 i**10 i**20 1 1 1 1 1 1 2 4 8 32 1024 1048576 3 9 27 243 59049 3486784401 4 16 64 1024 1048576 1099511627776 5 25 125 3125 9765625 95367431640625 6 36 216 7776 60466176 3656158440062976 7 49 343 16807 282475249 79792266297612001 8 64 512 32768 1073741824 1152921504606846976 9 81 729 59049 3486784401 12157665459056928801 10 100 1000 100000 10000000000 100000000000000000000
One possible solution would be to change the tab width, but the first column already has more space than it needs. The best solution would be to set the width of each column independently. As you may have guessed by now, string formatting provides a much nicer solution. We can also right-justify each field:
layout = "{0:>4}{1:>6}{2:>6}{3:>8}{4:>13}{5:>24}" print(layout.format("i", "i**2", "i**3", "i**5", "i**10", "i**20")) for i in range(1, 11): print(layout.format(i, i**2, i**3, i**5, i**10, i**20))
Running this version produces the following (much more satisfying) output:
i i**2 i**3 i**5 i**10 i**20 1 1 1 1 1 1 2 4 8 32 1024 1048576 3 9 27 243 59049 3486784401 4 16 64 1024 1048576 1099511627776 5 25 125 3125 9765625 95367431640625 6 36 216 7776 60466176 3656158440062976 7 49 343 16807 282475249 79792266297612001 8 64 512 32768 1073741824 1152921504606846976 9 81 729 59049 3486784401 12157665459056928801 10 100 1000 100000 10000000000 100000000000000000000
Summary
This chapter introduced a lot of new ideas. The following summary may prove helpful in remembering what you learned.
- indexing ([])
- Access a single character in a string using its position (starting from 0). Example: "This"[2] evaluates to "i".
- length function (len)
- Returns the number of characters in a string. Example: len("happy") evaluates to 5.
- for loop traversal (for)
Traversing a string means accessing each character in the string, one at a time. For example, the following for loop:
for ch in "Example": ...executes the body of the loop 7 times with different values of ch each time.
- slicing ([:])
- A slice is a substring of a string. Example: 'bananas and cream'[3:6] evaluates to ana (so does 'bananas and cream'[1:4]).
- string comparison (>, <, >=, <=, ==, !=)
- The six common comparison operators work with strings, evaluating according to lexicographical order. Examples: "apple" < "banana" evaluates to True. "Zeta" < "Appricot" evaluates to False. "Zebra" <= "aardvark" evaluates to True because all upper case letters precede lower case letters.
- in and not in operator (in, not in)
- The in operator tests for membership. In the case of strings, it tests whether one string is contained inside another string. Examples: "heck" in "I'll be checking for you." evaluates to True. "cheese" in "I'll be checking for you." evaluates to False.
Glossary
- compound data type
- A data type in which the values are made up of components, or elements, that are themselves values.
- default value
- The value given to an optional parameter if no argument for it is provided in the function call.
- docstring
- A string constant on the first line of a function or module definition (and as we will see later, in class and method definitions as well). Docstrings provide a convenient way to associate documentation with code. Docstrings are also used by programming tools to provide interactive help.
- dot notation
- Use of the dot operator, ., to access methods and attributes of an object.
- immutable data value
- A data value which cannot be modified. Assignments to elements or slices (sub-parts) of immutable values cause a runtime error.
- index
- A variable or value used to select a member of an ordered collection, such as a character from a string, or an element from a list.
- mutable data value
- A data value which can be modified. The types of all mutable values are compound types. Lists and dictionaries are mutable; strings and tuples are not.
- optional parameter
- A parameter written in a function header with an assignment to a default value which it will receive if no corresponding argument is given for it in the function call.
- short-circuit evaluation
- A style of programming that shortcuts extra work as soon as the outcome is know with certainty. In this chapter our find function returned as soon as it found what it was looking for; it didn't traverse all the rest of the items in the string.
- slice
- A part of a string (substring) specified by a range of indices. More generally, a subsequence of any sequence type in Python can be created using the slice operator (sequence[start:stop]).
- traverse
- To iterate through the elements of a collection, performing a similar operation on each.
- whitespace
- Any of the characters that move the cursor without printing visible characters. The constant string.whitespace contains all the white-space characters.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Lists
Source: this section is heavily based on Chapter 11 of [ThinkCS].
A list is an ordered collection of values. The values that make up a list are called its elements, or its items. We will use the term element or item to mean the same thing. Lists are similar to strings, which are ordered collections of characters, except that the elements of a list can be of any type. Lists and strings --- and other collections that maintain the order of their items --- are called sequences.
List values
There are several ways to create a new list; the simplest is to enclose the elements in square brackets ([ and ]):
ps = [10, 20, 30, 40] qs = ["spam", "bungee", "swallow"]
The first example is a list of four integers. The second is a list of three strings. The elements of a list don't have to be the same type. The following list contains a string, a float, an integer, and (amazingly) another list:
zs = ["hello", 2.0, 5, [10, 20]]
A list within another list is said to be nested.
Finally, a list with no elements is called an empty list, and is denoted [].
We have already seen that we can assign list values to variables or pass lists as parameters to functions:
>>> vocabulary = ["apple", "cheese", "dog"] >>> numbers = [17, 123] >>> an_empty_list = [] >>> print(vocabulary, numbers, an_empty_list) ["apple", "cheese", "dog"] [17, 123] []
Accessing elements
The syntax for accessing the elements of a list is the same as the syntax for accessing the characters of a string --- the index operator: [] (not to be confused with an empty list). The expression inside the brackets specifies the index. Remember that the indices start at 0:
>>> numbers[0] 17
Any expression evaluating to an integer can be used as an index:
>>> numbers[9-8] 5 >>> numbers[1.0] Traceback (most recent call last): File "<interactive input>", line 1, in <module> TypeError: list indices must be integers, not float
If you try to access or assign to an element that does not exist, you get a runtime error:
>>> numbers[2] Traceback (most recent call last): File "<interactive input>", line 1, in <module> IndexError: list index out of range
It is common to use a loop variable as a list index.
horsemen = ["war", "famine", "pestilence", "death"] for i in [0, 1, 2, 3]: print(horsemen[i])
Each time through the loop, the variable i is used as an index into the list, printing the i'th element. This pattern of computation is called a list traversal.
The above sample doesn't need or use the index i for anything besides getting the items from the list, so this more direct version --- where the for loop gets the items --- might be preferred:
horsemen = ["war", "famine", "pestilence", "death"] for h in horsemen: print(h)
List length
The function len returns the length of a list, which is equal to the number of its elements. If you are going to use an integer index to access the list, it is a good idea to use this value as the upper bound of a loop instead of a constant. That way, if the size of the list changes, you won't have to go through the program changing all the loops; they will work correctly for any size list:
horsemen = ["war", "famine", "pestilence", "death"] for i in range(len(horsemen)): print(horsemen[i])
The last time the body of the loop is executed, i is len(horsemen) - 1, which is the index of the last element. (But the version without the index looks even better now!)
Although a list can contain another list, the nested list still counts as a single element in its parent list. The length of this list is 4:
>>> len(["car makers", 1, ["Ford", "Toyota", "BMW"], [1, 2, 3]]) 4
List membership (Optional topic)
in and not in are Boolean operators that test membership in a sequence. We used them previously with strings, but they also work with lists and other sequences:
>>> horsemen = ["war", "famine", "pestilence", "death"] >>> "pestilence" in horsemen True >>> "debauchery" in horsemen False >>> "debauchery" not in horsemen True
Using this produces a more elegant version of the nested loop program we previously used to count the number of students doing Computer Science in the section nested_data:
students = [ ("John", ["CompSci", "Physics"]), ("Vusi", ["Maths", "CompSci", "Stats"]), ("Jess", ["CompSci", "Accounting", "Economics", "Management"]), ("Sarah", ["InfSys", "Accounting", "Economics", "CommLaw"]), ("Zuki", ["Sociology", "Economics", "Law", "Stats", "Music"])] # Count how many students are taking CompSci counter = 0 for (name, subjects) in students: if "CompSci" in subjects: counter += 1 print("The number of students taking CompSci is", counter)
List operations
The + operator concatenates lists:
>>> a = [1, 2, 3] >>> b = [4, 5, 6] >>> c = a + b >>> c [1, 2, 3, 4, 5, 6]
Similarly, the * operator repeats a list a given number of times:
>>> [0] * 4 [0, 0, 0, 0] >>> [1, 2, 3] * 3 [1, 2, 3, 1, 2, 3, 1, 2, 3]
The first example repeats [0] four times. The second example repeats the list [1, 2, 3] three times.
List slices
The slice operations we saw previously with strings let us work with sublists:
>>> a_list = ["a", "b", "c", "d", "e", "f"] >>> a_list[1:3] ['b', 'c'] >>> a_list[:4] ['a', 'b', 'c', 'd'] >>> a_list[3:] ['d', 'e', 'f'] >>> a_list[:] ['a', 'b', 'c', 'd', 'e', 'f']
Lists are mutable
Unlike strings, lists are mutable, which means we can change their elements. Using the index operator on the left side of an assignment, we can update one of the elements:
>>> fruit = ["banana", "apple", "quince"] >>> fruit[0] = "pear" >>> fruit[2] = "orange" >>> fruit ['pear', 'apple', 'orange']
The bracket operator applied to a list can appear anywhere in an expression. When it appears on the left side of an assignment, it changes one of the elements in the list, so the first element of fruit has been changed from "banana" to "pear", and the last from "quince" to "orange". An assignment to an element of a list is called item assignment. Item assignment does not work for strings:
>>> my_string = "TEST" >>> my_string[2] = "X" Traceback (most recent call last): File "<interactive input>", line 1, in <module> TypeError: 'str' object does not support item assignment
but it does for lists:
>>> my_list = ["T", "E", "S", "T"] >>> my_list[2] = "X" >>> my_list ['T', 'E', 'X', 'T']
With the slice operator we can update a whole sublist at once:
>>> a_list = ["a", "b", "c", "d", "e", "f"] >>> a_list[1:3] = ["x", "y"] >>> a_list ['a', 'x', 'y', 'd', 'e', 'f']
We can also remove elements from a list by assigning an empty list to them:
>>> a_list = ["a", "b", "c", "d", "e", "f"] >>> a_list[1:3] = [] >>> a_list ['a', 'd', 'e', 'f']
And we can add elements to a list by squeezing them into an empty slice at the desired location:
>>> a_list = ["a", "d", "f"] >>> a_list[1:1] = ["b", "c"] >>> a_list ['a', 'b', 'c', 'd', 'f'] >>> a_list[4:4] = ["e"] >>> a_list ['a', 'b', 'c', 'd', 'e', 'f']
List deletion
Using slices to delete list elements can be error-prone. Python provides an alternative that is more readable. The del statement removes an element from a list:
>>> a = ["one", "two", "three"] >>> del a[1] >>> a ['one', 'three']
As you might expect, del causes a runtime error if the index is out of range.
You can also use del with a slice to delete a sublist:
>>> a_list = ["a", "b", "c", "d", "e", "f"] >>> del a_list[1:5] >>> a_list ['a', 'f']
As usual, the sublist selected by slice contains all the elements up to, but not including, the second index.
Objects and references
After we execute these assignment statements
a = "banana" b = "banana"
we know that a and b will refer to a string object with the letters "banana". But we don't know yet whether they point to the same string object.
There are two possible ways the Python interpreter could arrange its memory:
In one case, a and b refer to two different objects that have the same value. In the second case, they refer to the same object.
We can test whether two names refer to the same object using the is operator:
>>> a is b True
This tells us that both a and b refer to the same object, and that it is the second of the two state snapshots that accurately describes the relationship.
Since strings are immutable, Python optimizes resources by making two names that refer to the same string value refer to the same object.
This is not the case with lists:
>>> a = [1, 2, 3] >>> b = [1, 2, 3] >>> a == b True >>> a is b False
The state snapshot here looks like this:
a and b will then have the same value but do not refer to the same object.
Aliasing
Since variables refer to objects, if we assign one variable to another, both variables refer to the same object:
>>> a = [1, 2, 3] >>> b = a >>> a is b True
In this case, the state snapshot looks like this:
Because the same list has two different names, a and b, we say that it is aliased. Changes made with one alias affect the other:
>>> b[0] = 5 >>> a [5, 2, 3]
Although this behavior can be useful, it is sometimes unexpected or undesirable. In general, it is safer to avoid aliasing when you are working with mutable objects (i.e. lists at this point in our textbook, but we'll meet more mutable objects as we cover classes and objects, dictionaries and sets). Of course, for immutable objects (i.e. strings), there's no problem --- it is just not possible to change something and get a surprise when you access an alias name. That's why Python is free to alias strings (and any other immutable kinds of data) when it sees an opportunity to economize.
Cloning lists
If we want to modify a list and also keep a copy of the original, we need to be able to make a copy of the list itself, not just the reference. This process is sometimes called cloning, to avoid the ambiguity of the word copy.
The easiest way to clone a list is to use the slice operator:
>>> a = [1, 2, 3] >>> b = a[:] >>> b [1, 2, 3]
Taking any slice of a creates a new list. In this case the slice happens to consist of the whole list. So now the relationship is like this:
Now we are free to make changes to b without worrying that we'll inadvertently be changing a:
>>> b[0] = 5 >>> a [1, 2, 3]
Lists and for loops
The for loop also works with lists, as we've already seen. The generalized syntax of a for loop is:
for VARIABLE in LIST: BODY
So, as we've seen
friends = ["Joe", "Zoe", "Brad", "Angelina", "Zuki", "Thandi", "Paris"] for friend in friends: print(friend)
It almost reads like English: For (every) friend in (the list of) friends, print (the name of the) friend.
Any list expression can be used in a for loop:
for number in range(20): if number % 3 == 0: print(number) for fruit in ["banana", "apple", "quince"]: print("I like to eat " + fruit + "s!")
The first example prints all the multiples of 3 between 0 and 19. The second example expresses enthusiasm for various fruits.
Since lists are mutable, we often want to traverse a list, changing each of its elements. The following squares all the numbers in the list xs:
xs = [1, 2, 3, 4, 5] for i in range(len(xs)): xs[i] = xs[i]**2
Take a moment to think about range(len(xs)) until you understand how it works.
List parameters
Passing a list as an argument actually passes a reference to the list, not a copy or clone of the list. So parameter passing creates an alias for you: the caller has one variable referencing the list, and the called function has an alias, but there is only one underlying list object. For example, the function below takes a list as an argument and multiplies each element in the list by 2:
def double_stuff(a_list): """ Overwrite each element in a_list with double its value. """ for i in range(len(a_list)): a_list[i] = 2 * a_list[i]
If we add the following onto our script:
things = [2, 5, 9] double_stuff(things) print(things)
When we run it we'll get:
[4, 10, 18]
In the function above, the parameter a_list and the variable things are aliases for the same object. So before any changes to the elements in the list, the state snapshot looks like this:
Since the list object is shared by two frames, we drew it between them.
If a function modifies the items of a list parameter, the caller sees the change.
Use the Python visualizer!
We've already mentioned the Python visualizer at http://www.pythontutor.com/visualize.html. It is a very useful tool for building a good understanding of references, aliases, assignments, and passing arguments to functions. Pay special attention to cases where you clone a list or have two separate lists, and cases where there is only one underlying list, but more than one variable is aliased to reference the list.
List methods
The dot operator can also be used to access built-in methods of list objects. We'll start with the most useful method for adding something onto the end of an existing list:
>>> mylist = [] >>> mylist.append(5) >>> mylist.append(27) >>> mylist.append(3) >>> mylist.append(12) >>> mylist [5, 27, 3, 12]
append is a list method which adds the argument passed to it to the end of the list. We'll use it heavily when we're creating new lists. Continuing with this example, we show several other list methods:
>>> mylist.insert(1, 12) # Insert 12 at pos 1, shift other items up >>> mylist [5, 12, 27, 3, 12] >>> mylist.count(12) # How many times is 12 in mylist? 2 >>> mylist.extend([5, 9, 5, 11]) # Put whole list onto end of mylist >>> mylist [5, 12, 27, 3, 12, 5, 9, 5, 11]) >>> mylist.index(9) # Find index of first 9 in mylist 6 >>> mylist.reverse() >>> mylist [11, 5, 9, 5, 12, 3, 27, 12, 5] >>> mylist.sort() >>> mylist [3, 5, 5, 5, 9, 11, 12, 12, 27] >>> mylist.remove(12) # Remove the first 12 in the list >>> mylist [3, 5, 5, 5, 9, 11, 12, 27]
Experiment and play with the list methods shown here, and read their documentation until you feel confident that you understand how they work. You are not required to learn these functions by heart and are always free to check Python's documentation to understand what these functions are doing.
Python also provides built-in functions that can be applied to lists. One example is the sorted function.
>>> mylist = [5, 27, 3, 12] >>> sorted ( mylist ) [3, 5, 1, 27] >>> mylist [5, 27, 3, 12]
The difference between sorted and sort is that sorted returns a sorted version of the list, and keeps the original list unmodified.
Pure functions and modifiers
Functions which take lists as arguments and change them during execution are called modifiers and the changes they make are called side effects.
A pure function does not produce side effects. It communicates with the calling program only through parameters, which it does not modify, and a return value. Here is double_stuff written as a pure function:
def double_stuff(a_list): """ Return a new list which contains doubles of the elements in a_list. """ new_list = [] for value in a_list: new_elem = 2 * value new_list.append(new_elem) return new_list
This version of double_stuff does not change its arguments:
>>> things = [2, 5, 9] >>> xs = double_stuff(things) >>> things [2, 5, 9] >>> xs [4, 10, 18]
An early rule we saw for assignment said "first evaluate the right hand side, then assign the resulting value to the variable". So it is quite safe to assign the function result to the same variable that was passed to the function:
>>> things = [2, 5, 9] >>> things = double_stuff(things) >>> things [4, 10, 18]
Which style is better?
Anything that can be done with modifiers can also be done with pure functions. In fact, some programming languages only allow pure functions. There is some evidence that programs that use pure functions are faster to develop and less error-prone than programs that use modifiers. Nevertheless, modifiers are convenient at times, and in some cases, functional programs are less efficient.
In general, we recommend that you write pure functions whenever it is reasonable to do so and resort to modifiers only if there is a compelling advantage. This approach might be called a functional programming style.
Functions that produce lists
The pure version of double_stuff above made use of an important pattern for your toolbox. Whenever you need to write a function that creates and returns a list, the pattern is usually:
initialize a result variable to be an empty list loop create a new element append it to result return the result
Let us show another use of this pattern. Assume you already have a function is_prime(x) that can test if x is prime. Write a function to return a list of all prime numbers less than n:
def primes_lessthan(n): """ Return a list of all prime numbers less than n. """ result = [] for i in range(2, n): if is_prime(i): result.append(i) return result
Strings and lists (Optional topic)
Two useful methods on strings involve conversion to and from lists of substrings. We will see these in more detail when discussing how to read files; however, feel free to read a little about them at this moment already. The split method breaks a string into a list of words. By default, any number of whitespace characters is considered a word boundary:
>>> song = "The rain in Spain..." >>> wds = song.split() >>> wds ['The', 'rain', 'in', 'Spain...']
An optional argument called a delimiter can be used to specify which string to use as the boundary marker between substrings. The following example uses the string ai as the delimiter:
>>> song.split("ai") ['The r', 'n in Sp', 'n...']
Notice that the delimiter doesn't appear in the result.
The inverse of the split method is join. You choose a desired separator string, (often called the glue) and join the list with the glue between each of the elements:
>>> glue = ";" >>> s = glue.join(wds) >>> s 'The;rain;in;Spain...'
The list that you glue together (wds in this example) is not modified. Also, as these next examples show, you can use empty glue or multi-character strings as glue:
>>> " --- ".join(wds) 'The --- rain --- in --- Spain...' >>> "".join(wds) 'TheraininSpain...'
list and range
Python has a built-in type conversion function called list that tries to turn whatever you give it into a list.
>>> xs = list("Crunchy Frog") >>> xs ["C", "r", "u", "n", "c", "h", "y", " ", "F", "r", "o", "g"] >>> "".join(xs) 'Crunchy Frog'
One particular feature of range is that it doesn't instantly compute all its values: it "puts off" the computation, and does it on demand, or "lazily". We'll say that it gives a promise to produce the values when they are needed. This is very convenient if your computation short-circuits a search and returns early, as in this case:
def f(n): """ Find the first positive integer between 101 and less than n that is divisible by 21 """ for i in range(101, n): if (i % 21 == 0): return i test(f(110) == 105) test(f(1000000000) == 105)
In the second test, if range were to eagerly go about building a list with all those elements, you would soon exhaust your computer's available memory and crash the program. But it is cleverer than that! This computation works just fine, because the range object is just a promise to produce the elements if and when they are needed. Once the condition in the if becomes true, no further elements are generated, and the function returns. (Note: Before Python 3, range was not lazy. If you use an earlier versions of Python, YMMV!)
YMMV: Your Mileage May Vary
The acronym YMMV stands for your mileage may vary. American car advertisements often quoted fuel consumption figures for cars, e.g. that they would get 28 miles per gallon. But this always had to be accompanied by legal small-print warning the reader that they might not get the same. The term YMMV is now used idiomatically to mean "your results may differ", e.g. The battery life on this phone is 3 days, but YMMV.
You'll sometimes find the lazy range wrapped in a call to list. This forces Python to turn the lazy promise into an actual list:
>>> range(10) # Create a lazy promise range(0, 10) >>> list(range(10)) # Call in the promise, to produce a list. [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
List Comprehension (Optional topic)
Let us reconsider the double_stuff function:
def double_stuff(a_list): """ Return a new list which contains doubles of the elements in a_list. """ new_list = [] for value in a_list: new_elem = 2 * value new_list.append(new_elem) return new_list
While this function is correct, the developers of Python felt that this notation is longer than desirable: in Python one often wishes to create lists based on other lists. For this reason, a shorter notation was introduced in the language. Any program written using this shorter notation, can also be written without it; however, programs much shorter when you use it:
def double_stuff(a_list): """ Return a new list which contains doubles of the elements in a_list. """ return [ 2 * value for value in a_list ]
This notation is known as list comprehension, and is inspired by set-builder notation in mathematics. An equivalent way of writing in mathematics is the following:
In mathematics we can also write statements such as this:
Also this can be transformed directly into Python!
def double_stuff(a_list): """ Return a new list which contains doubles of the elements in a_list that are not lower than 3 """ return [ 2 * value for value in a_list if a>= 3 ]
We can use multiple nested loops in list comprehension as well:
[ x * y for x in [0,1,2] for y in [0,2,4] if x * y >= 3 ]
In mathematics, we would write this as follows:
List comprehension is useful in many contexts. One interesting example in which we can use list comprehension is in the conversion of lists. Suppose we have this list of numbers:
numbers = [1, 3, 5]
and we wish to turn this list into the following strings:
["1", "3", "5"]
Unfortunately, we cannot obtain this string by simply writing str(numbers). The result of str(numbers) is a single string that represents the list of numbers.
To convert every element in a list separately, we can however write:
[ str(number) for number in numbers ]
Here, we apply the str function on every number in the numbers list, and put the result of this function call in the new list.
Glossary
- aliases
- Multiple variables that contain references to the same object.
- clone
- To create a new object that has the same value as an existing object. Copying a reference to an object creates an alias but doesn't clone the object.
- delimiter
- A character or string used to indicate where a string should be split.
- element
- One of the values in a list (or other sequence). The bracket operator selects elements of a list. Also called item.
- immutable data value
- A data value which cannot be modified. Assignments to elements or slices (sub-parts) of immutable values cause a runtime error.
- index
- An integer value that indicates the position of an item in a list. Indexes start from 0.
- item
- See element.
- list
- A collection of values, each in a fixed position within the list. Like other types str, int, float, etc. there is also a list type-converter function that tries to turn whatever argument you give it into a list.
- list traversal
- The sequential accessing of each element in a list.
- modifier
- A function which changes its arguments inside the function body. Only mutable types can be changed by modifiers.
- mutable data value
- A data value which can be modified. The types of all mutable values are compound types. Lists and dictionaries are mutable; strings and tuples are not.
- nested list
- A list that is an element of another list.
- object
- A thing to which a variable can refer.
- pattern
- A sequence of statements, or a style of coding something that has general applicability in a number of different situations. Part of becoming a mature Computer Scientist is to learn and establish the patterns and algorithms that form your toolkit. Patterns often correspond to your "mental chunking".
- promise
- An object that promises to do some work or deliver some values if they're eventually needed, but it lazily puts off doing the work immediately. Calling range produces a promise.
- pure function
- A function which has no side effects. Pure functions only make changes to the calling program through their return values.
- sequence
- Any of the data types that consist of an ordered collection of elements, with each element identified by an index.
- side effect
- A change in the state of a program made by calling a function. Side effects can only be produced by modifiers.
- step size
- The interval between successive elements of a linear sequence. The third (and optional argument) to the range function is called the step size. If not specified, it defaults to 1.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Nested Datastructures
Source: this section combines elements of Chapters 7 and 11 of [ThinkCS].
In the previous sections, we introduced strings and lists as individual data structures. In practice, these data structures are often used in combination with each other. We will show a number of such cases in this section.
Nested lists
A nested list is a list that appears as an element in another list. In this list, the element with index 3 is a nested list:
>>> nested = ["hello", 2.0, 5, [10, 20]]
If we output the element at index 3, we get:
>>> print(nested[3]) [10, 20]
To extract an element from the nested list, we can proceed in two steps:
>>> elem = nested[3] >>> elem[0] 10
Or we can combine them:
>>> nested[3][1] 20
Bracket operators evaluate from left to right, so this expression gets the 3'th element of nested and extracts the 1'th element from it.
Matrices
Nested lists are often used to represent matrices. For example, consider this matrix:
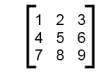 >>> mx = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
>>> mx = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
mx is a list with three elements, where each element is a row of the matrix. We can select an entire row from the matrix in the usual way:
>>> mx[1] [4, 5, 6]
Or we can extract a single element from the matrix using the double-index form:
>>> mx[1][2] 6
The first index selects the row, and the second index selects the column. Although this way of representing matrices is common, it is not the only possibility. A small variation is to use a list of columns instead of a list of rows. Later we will see a more radical alternative using a dictionary.
An interesting question is how we can create a matrix of arbitrary size in a practical manner. Many solutions are possible, some of which are more readable than others. This is full code that creates a matrix using the append method:
def matrix(n): """ Returns an n times n matrix with zeros, represented using lists within lists """ m = [] for j in range(n): l = [] for i in range(n): l.append ( 0 ) m.append ( l ) return m
In this code, m is the matrix we are going to return. Within this list, we are creating n nested lists. Each of these nested lists is a list of n 0s.
It could be tempting to write this code instead:
def matrix_incorrect(n): l = [] for i in range(n): l.append ( 0 ) m = [] for j in range(n): m.append ( l ) return m
At first sight, it may seem that this code is correct. If you execute print(matrix_incorrect(3)) you will indeed see this output:
[[0, 0, 0], [0, 0, 0], [0, 0, 0]]
However, the data structure created by this function has undesirable properties. If we execute the following code:
m = matrix_incorrect(3) m[0][0] = 1 print(m)
we will see the following output:
[[1, 0, 0], [1, 0, 0], [1, 0, 0]]
This is most likely not the output that you were looking for; indeed, any modification of one row, will also lead to a modification of the other rows.
The explanation for this can be found in how Python deals with objects and references. The append method takes as argument a reference to an object, and will add a reference to this object to the list. In our code, we have first created a list for which l is a reference. Subsequently, we add this reference three times to the list m. As a result, all three elements in the list m point towards the same underlying list. As m[0], m[1], m[2] all point towards the same list, any change to m[0] will also be visible when printing m[1] and m[2].
Our original code did not have this problem, as we created a new nested list n times.
The following code would avoid this problem:
def matrix_incorrect(n): l = [] for i in range(n): l.append ( 0 ) m = [] for j in range(n): m.append ( list(l) ) return m
The main difference is here that we use the list(l) construction. This construction will first create a copy of l: it will create a new list object that contains the same elements as l; the reference to this new object is added t the list m. As we create n copies of the original list l, all these nested lists are now independent of each other.
Glossary
- nested list
- A list that is an element of another list.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Tuples
Source: this section is heavily based on Chapter 9 of [ThinkCS].
Tuples are used for grouping data
We saw earlier that we could group together pairs of values by surrounding with parentheses. Recall this example:
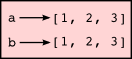
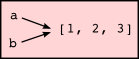
>>> year_born = ("Paris Hilton", 1981)
The pair is an example of a tuple. This is an example of a data structure --- a mechanism for grouping and organizing data to make it easier to use. Generalizing this, a tuple can be used to group any number of items into a single compound value. Syntactically, a tuple is a comma-separated sequence of values. Although it is not necessary, it is conventional to enclose tuples in parentheses:
>>> julia = ("Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia")
Tuples are useful for representing what other languages often call records --- some related information that belongs together, like your student record. There is no description of what each of these fields means, but we can guess. A tuple lets us "chunk" together related information and use it as a single thing.
Tuples are very similar to lists and support the same sequence operations as lists. The index operator selects an element from a tuple:
>>> julia[2] 1967
However, tuples are not the same as lists. Next to the different syntax (parentheses instead of square brackets), an important difference is that tuples are unmutable. If we try to use item assignment to modify one of the elements of the tuple, we get an error:
>>> julia[0] = "X" TypeError: 'tuple' object does not support item assignment
Similarly, we can not add elemnts to a tuple, or remove them; once Python has created a tuple in memory, it cannot be changed.
Of course, even if we can't modify the elements of a tuple, we can always make the julia variable reference a new tuple holding different information. To construct the new tuple, it is convenient that we can slice parts of the old tuple and join up the bits to make the new tuple. So if julia has a new recent film, we could change her variable to reference a new tuple that used some information from the old one:
>>> julia = julia[:3] + ("Eat Pray Love", 2010) + julia[5:] >>> julia ("Julia", "Roberts", 1967, "Eat Pray Love", 2010, "Actress", "Atlanta, Georgia")
To create a tuple with a single element (but you're probably not likely to do that too often), we have to include the final comma, because without the final comma, Python treats the (5) below as an integer in parentheses:
>>> tup = (5,) >>> type(tup) <class 'tuple'> >>> x = (5) >>> type(x) <class 'int'>
Given the similarity between Python's tuples and lists, a good question is why tuples exist at all. Why doesn't Python only have lists? There are two good reasons for the existence of tuples.
One is the performance of the code. Tuples are more efficient than lists: they consume less memory and the run time required to create them is smaller.
Why is this? We skimmed over this till now, but allocating memory in a computer is not a trivial operation; essentially, each time a program requires more memory, the operating system will have to search for a piece of memory that is still unused. This also applies to lists. If the operating system would have to look for a new piece memory each time an element is added to a list, adding elements to a list would be a rather slow operation. To avoid this, Python tries to be intelligent: it will anticipate the addition of elements in a list by reserving more memory than necessary at the moment of creation. The benefit is that adding elements is now faster. The side effect is however that lists will consume more memory than necessary. Python's tuples avoid this. As a tuple will never change, we know its memory consumption will never change. Hence, Python does not need to anticipate future additions to the tuple.
The second reason for having tuples relates to the readability of code written using tuples. Consider this piece of code:
julia = ("Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia") do_something ( julia ) print ( julia[0] )
For this piece of code, we can be sure that whatever the functionality of the function do_something is, at the end the string "Julia" will be printed. This makes it easy to understand what the third line of code is doing.
Consider now this piece of code:
julia = ["Julia", "Roberts", 1967, "Duplicity", 2009, "Actress", "Atlanta, Georgia"] do_something ( julia ) print ( julia[0] )
In this code, we can no longer be sure about what julia[0] will print. Consider this implementation of the do_something function:
def do_something ( l ): l[0] = "Hugh"
This function will change the list julia, and as a result the code will print "Hugh". Hence, to understand what the line print ( julia[0] ) does, we will need to check the documentation or source code of the function do_something. For tuples, this is not necessary: by using tuples, the programmer can communicate to another reader of the code that this data is not supposed to be changed. Indeed, any function that you will apply on this tuple, and that would try to change it, will yield an error message, hence making it easier to debug the code as well.
Tuple assignments
Python has a very powerful tuple assignment feature that allows a tuple of variables on the left of an assignment to be assigned values from a tuple on the right of the assignment. (We already saw this used for pairs, but it generalizes.)
(name, surname, b_year, movie, m_year, profession, b_place) = julia
This can also be shortened to
name, surname, b_year, movie, m_year, profession, b_place = julia
This does the equivalent of seven assignment statements, all on one easy line. One requirement is that the number of variables on the left must match the number of elements in the tuple.
One way to think of tuple assignment is as tuple packing/unpacking.
In tuple packing, the values on the left are 'packed' together in a tuple:
>>> b = ("Bob", 19, "CS") # tuple packing
In tuple unpacking, the values in a tuple on the right are 'unpacked' into the variables/names on the right:
>>> b = ("Bob", 19, "CS") >>> (name, age, studies) = b # tuple unpacking >>> name 'Bob' >>> age 19 >>> studies 'CS'
Once in a while, it is useful to swap the values of two variables. With conventional assignment statements, we have to use a temporary variable. For example, to swap a and b:
temp = a a = b b = temp
Tuple assignment solves this problem neatly:
a, b = b, a
The left side is a tuple of variables; the right side is a tuple of values. Each value is assigned to its respective variable. All the expressions on the right side are evaluated before any of the assignments. This feature makes tuple assignment quite versatile.
Naturally, the number of variables on the left and the number of values on the right have to be the same:
>>> (a, b, c, d) = (1, 2, 3) ValueError: need more than 3 values to unpack
Tuples as return values
Functions can always only return a single value, but by making that value a tuple, we can effectively group together as many values as we like, and return them together. This is very useful --- we often want to know some batsman's highest and lowest score, or we want to find the mean and the standard deviation, or we want to know the year, the month, and the day, or if we're doing some some ecological modelling we may want to know the number of rabbits and the number of wolves on an island at a given time.
For example, we could write a function that returns both the area and the circumference of a circle of radius r:
def f(r): """ Return (circumference, area) of a circle of radius r """ c = 2 * math.pi * r a = math.pi * r * r return (c, a)
Composability of Data Structures
We saw in an earlier chapter that we could make a list of pairs, and we had an example where one of the items in the tuple was itself a list:
students = [ ("John", ["CompSci", "Physics"]), ("Vusi", ["Maths", "CompSci", "Stats"]), ("Jess", ["CompSci", "Accounting", "Economics", "Management"]), ("Sarah", ["InfSys", "Accounting", "Economics", "CommLaw"]), ("Zuki", ["Sociology", "Economics", "Law", "Stats", "Music"])]
Tuples items can themselves be other tuples. For example, we could improve the information about our movie stars to hold the full date of birth rather than just the year, and we could have a list of some of her movies and dates that they were made, and so on:
julia_more_info = ( ("Julia", "Roberts"), (8, "October", 1967), "Actress", ("Atlanta", "Georgia"), [ ("Duplicity", 2009), ("Notting Hill", 1999), ("Pretty Woman", 1990), ("Erin Brockovich", 2000), ("Eat Pray Love", 2010), ("Mona Lisa Smile", 2003), ("Oceans Twelve", 2004) ])
Notice in this case that the tuple has just five elements --- but each of those in turn can be another tuple, a list, a string, or any other kind of Python value. This property is known as being heterogeneous, meaning that it can be composed of elements of different types.
Functions Generating Lists of Tuples (Optional topic)
We have already seen the following code:
xs = [1, 2, 3, 4, 5] for i in range(len(xs)): xs[i] = xs[i]**2
While correct, this type of list traversal is so common, that Python provides a nicer way to implement it:
xs = [1, 2, 3, 4, 5] for (i, val) in enumerate(xs): xs[i] = val**2
This code exploits lists-of-tuples: enumerate generates pairs of both (index, value) during the list traversal. Try this next example to see more clearly how enumerate works:
for (i, v) in enumerate(["banana", "apple", "pear", "lemon"]): print(i, v)0 banana 1 apple 2 pear 3 lemon
Another common type of program one may wish to write is the following:
xs = [1, 2, 3, 4, 5] ys = [3, 4, 5, 6, 7] for i in range(len(xs)): print (xs[i],ys[i])
Using the enumerate function we could rewrite this as:
xs = [1, 2, 3, 4, 5] ys = [3, 4, 5, 6, 7] for (i, val) in enumerate(xs): print (val,ys[i])
However, most programmers would not consider this to be a very clean solution. Python provides the zip function to write this code more elegantly:
xs = [1, 2, 3, 4, 5] ys = [3, 4, 5, 6, 7] for x, y in zip(xs,ys): print (x,y)
Like a zipper, the zip function combines elements of two given lists pairwise, and provides a list of the tuples that represent pairs from the two given list.
In combination with the enumerate function, one can now write code like the following:
xs = [1, 2, 3, 4, 5] ys = [3, 4, 5, 6, 7] for i, (x, y) in enumerate(zip(xs,ys)): xs[i] = x**2 ys[i] = y**2
Observe that in this code, the zip function generates pairs of elements from the xs and ys lists. The enumerate function subsequently adds the indexes of the pairs in this list.
Glossary
- data structure
- An organization of data for the purpose of making it easier to use.
- immutable data value
- A data value which cannot be modified. Assignments to elements or slices (sub-parts) of immutable values cause a runtime error.
- mutable data value
- A data value which can be modified. The types of all mutable values are compound types. Lists and dictionaries are mutable; strings and tuples are not.
- tuple
- An immutable data value that contains related elements. Tuples are used to group together related data, such as a person's name, their age, and their gender.
- tuple assignment
- An assignment to all of the elements in a tuple using a single assignment statement. Tuple assignment occurs simultaneously rather than in sequence, making it useful for swapping values.
- heterogeneous list
- A list that contains elements of different types.
- generators
- Functions that will generate lists
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Specifications and Tests
Source: this section is not based on external sources.
The main purpose of coding is to create an executable program. Code should however not only execute; it should also satisfy a number of additional requirements:
- it should be correct: it should do what it is expected to do;
- it should be readable: others should be able to easily understand it;
- it should be maintainable: it should be easy to add features, remove features, correct problems.
To understand the importance of these requirements, consider the following sitations:
- You wish to add a feature to a program that you wrote one year ago.
- You write a program that a collaborator needs to modify later on.
- You are contacted about a bug in a program that you wrote a year ago.
- You wish to add a feature to a library written by somebody else.
- You are asked to maintain source code that was written by somebody else.
In all these cases, it is not only important that code executes; it is also important that your code is of sufficiently good quality to support these other requirements. Writing code of good quality is not easy. Some programmers that understand Python very well, will still write code that is very hard to read. Consider this fragment of bad code:
f=type((lambda:(lambda:None for n in range(len(((((),(((),())))))))))().next()) u=(lambda:type((lambda:(lambda:None for n in range(len(zip((((((((())))))))))))).func_code))() n=f(u(int(wwpd[4][1]),int(wwpd[7][1]),int(wwpd[6][1]),int(wwpd[9][1]),wwpd[2][1], (None,wwpd[10][1],wwpd[13][1],wwpd[11][1],wwpd[15][1]),(wwpd[20][1],wwpd[21][1]), (wwpd[16][1],wwpd[17][1],wwpd[18][1],wwpd[11][1],wwpd[19][1]),wwpd[22][1],wwpd[25][1],int(wwpd[4][1]),wwpd[0][1]), {wwpd[27][1]:__builtins__,wwpd[28][1]:wwpd[29][1]}) c=partial(n, [x for x in map(lambda i:n(i),range(int(0xbeef)))]) FIGHT = f(u(int(wwpd[4][1]),int(wwpd[4][1]),int(wwpd[5][1]),int(wwpd[9][1]),wwpd[3][1], (None, wwpd[23][1]), (wwpd[14][1],wwpd[24][1]),(wwpd[12][1],),wwpd[22][1],wwpd[26][1],int(wwpd[8][1]),wwpd[1][1]), {wwpd[14][1]:c,wwpd[24][1]:urlopen,wwpd[27][1]:__builtins__,wwpd[28][1]:wwpd[29][1]}) FIGHT(msg)
Maintaining, modifying or building on this code is very difficult, even for the most experienced programmer. Hence, it is important that while you learn how to program, you also pay attention to how to write good code. We don't want you to create code such as the one in this example!
In this chapter, we will introduce you to the practice of writing specifications for the functions used in a program, followed by tests that check whether the source code meets the specifications.
Specifications in Python
Consider the following code:
def f ( n ): for i in range(1,n): if n % i == 0: return False return True
We could try to read this code in order to understand it. However, this would require quite some effort from every programmer using this function. Better is to give the function an interpretable name and add documentation; as we have seen earlier in this syllabus, we can do so by adding a block of comments after the function definition:
def prime ( n ): """ Return whether the number n is prime """ for i in range(1,n): if n % i == 0: return False return True
This code is already easier to understand. However, its documentation is still not very precise. For instance, the user of the code could wonder whether it is possible to execute this code for n=0, =-1, or n=0.5. In many projects it is desirable to make the specification of each parameter as precise as possible. One way of doing this is as follows:
def prime ( n ): """ pre: n an integer >= 1 post: true if the number n is prime """ for i in range(1,n): if n % i == 0: return False return True
In this case we have used the docstring to make the specification more precise.
In principle, we are completely free to write anything we want in a docstring; by default, Python does not look at the content of the docstring. It is hence possible to write anything that helps to understand the code.
In most parts of this course, we will use preconditions and postconditions to specify the functionality of a function in more detail. Specifications of preconditions and postconditions are precise, but not too long either.
In practice, larger software projects impose even more structure on the content of docstrings. One approach that is often used is that of Google Style docstrings, which were originally used by Google in its Python projects, but which are now also used in many other projects. The following code illustrates a Google Style docstring:
def prime ( n ): """ Determines whether n is a prime number. This function determines whether the positive integer n is a prime number. Args: n: a positive integer Returns: A boolean indicating whether n is a prime number. """ for i in range(2,n): if n % i == 0: return False return True
The structure of a Google Style Python docstring is always similar:
def function name ( arguments ): """ One short line describing the function. Longer text to describe the function. Args: argument name 1: short type description, with a short description ... (all arguments are described) ... argument name n: short type description, with a short description Returns: A short description of what the function returns. """ function code
Here is another example:
def zipper ( l1, l2 ): """ Zips two lists, such that elements of l1 and l2 are interleaved. This function zips two given lists l1 and l2 into a new list [l1[0],l2[0],l1[1],l2[1],...,l1[n],l2[n]], where l1 and l2 must be lists of equal length n. For example, zipper ( [1,2], [3,4] ) will return [1,3,2,4]. Args: l1: a list of length n l2: a list of the same length as l1 Returns: A new list with elements [l1[0],l2[0],l1[1],l2[1],...,l1[n],l2[n]] """ new_list = [] for i in range ( len ( l1 ) ): new_list.append ( l1[i] ) new_list.append ( l2[i] ) return new_list
Note that the docstring in this example is very verbose. In practice, one will not encounter such long docstrings for many short functions. Still, many programmers consider such long documentation the best approach. In this course we will from time to time ask you explicitly to provide such long Google Style docstrings; where this is not indicated explicitly, you may write shorter docstrings, such as using pre- and postconditions. However, you are always expected to provide an informative docstring.
Tests in Python
Now that we know how to write a proper specification for a function in Python, the next question is how we ensure that code satisfies the requirements specified in the docstring. A very common approach (that we will also use during the exams) is that of running unit tests. An unit test is a piece of code that tests whether a function operates as intended. This is an example of one unit test, for the prime function provided above:
if prime ( 10 ) == True: print ( "Error: 10 is not prime" )
This code runs the prime function and evaluates its return value: if the function returns True it has made an error, and we display an error message.
Note that there are many implementations of the prime function that will pass this test, while they are incorrect. For instance, this code will not give an error for the test case:
def prime ( n ): return False
Clearly, one test does not suffice to prove that an implementation of prime is correct.
The most straightforward solution to reduce the chances that an incorrect implementation is considered to be correct, is to write multiple tests:
if prime ( 10 ) == True: print ( "Error: 10 should not be prime" ) if prime ( 8 ) == True: print ( "Error: 8 should not be prime" ) if prime ( 5 ) == False: print ( "Error: 5 should be prime" ) if prime ( 3 ) == False: print ( "Error: 3 should be prime" ) if prime ( 997 ) == False: print ( "Error: 997 should be prime" )
How many test cases do we need to provide to test a function?
To answer this question, you will need to know more about theoretical computer science; you will need to study questions of computability. This is the subject of another course and will not be discussed in detail here. However, important to know is that in general, it is impossible to determine a finite set of tests to determine the correctness of a function that accepts a large number of different inputs. Hence, while tests can provide strong evidence that a function is implemented correctly, they are never sufficient evidence. In practice if often happens that you start with a small set of tests, while you discover later on that the code is still incorrect. In this case, the proper approach is to test cases.
Writing tests is so common in Python, that Python provides special notation to simplify their specification. A common approach is the one offered by the unittest module; however, you will need to know more about Python before you will be able to use this module. For most of this course, we will therefore rely on a more simple approach that is provided by the assert statement. Using this statement, the earlier set of tests can be written more compactly:
assert prime ( 10 ) == False, "10 should not be prime" assert prime ( 8 ) == False, "8 should not be prime" assert prime ( 5 ) == True, "5 should be prime" assert prime ( 3 ) == True, "3 should be prime" assert prime ( 997 ) == True, "997 should be prime"
Or even shorter:
assert not prime ( 10 ), "10 should not be prime" assert not prime ( 8 ), "8 should not be prime" assert prime ( 5 ), "5 should be prime" assert prime ( 3 ), "3 should be prime" assert prime ( 997 ), "997 should be prime"
If we execute this code for an incorrect impementation of prime, Python will give a message such as this one:
Traceback (most recent call last): File "test.py", line 20, in <module> assert prime ( 5 ) == True, "5 should be prime" AssertionError: 5 should be prime
The execution of the code will stop immediately at the test case that fails. Hence, for any given assert statement, Python will test whether the condition provided is satisfied; if not, it will print the message provided and will stop the execution immediately.
For our zipper function we can now write test cases in a similar fashion:
assert zipper ( [1,2], [3,4] ) == [1,3,2,4], "[1,2], [3,4] not zipped correctly" assert zipper ( [1,1,1], [2,2,2] ) == [1,2,1,2,1,2], "[1,2,1,2,1,2] not zipped correctly" assert zipper ( [100,300], [400,200] ) == [100,400,300,200], "[100,300], [400,200] not zipped correctly"
Note that these cases only test lists of lengths smaller than 3; it could be good to add some larger test cases as well to reduce the chances that an incorrect implementation still passes all the tests.
We could put a function and its tests in one file, as follows:
def prime ( n ): """ Determines whether n is a prime number. This function determines whether the positive integer n is a prime number. Args: n: a positive integer Returns: A boolean indicating whether n is a prime number. """ return True assert not prime ( 10 ), "10 should not be prime" assert not prime ( 8 ), "8 should not be prime" assert prime ( 5 ), "5 should be prime" assert prime ( 3 ), "3 should be prime" assert prime ( 997 ), "997 should be prime"
If we execute this code, we will get one error message before the code terminates. For a correct implementation of the prime function, the code will execute without printing a message.
Testing becomes slightly more complex if we wish to separate a program and its tests in separate files. Suppose we have this program, stored in a file prime.py:
def prime ( n ): """ Determines whether n is a prime number. This function determines whether the positive integer n is a prime number. Args: n: a positive integer Returns: A boolean indicating whether n is a prime number. """ return True for i in range ( 100 ): print ( i, prime ( i ) )
How can we test the prime function in a separate program? We could consider writing a second program, as follows:
from prime import * assert not prime ( 10 ), "10 should not be prime" assert not prime ( 8 ), "8 should not be prime" assert prime ( 5 ), "5 should be prime" assert prime ( 3 ), "3 should be prime" assert prime ( 997 ), "997 should be prime"
However, this code has undesirable behavior: when executing the import statement, it will also execute the print statements in the prime.py program. The reason for this is that when executing the import statement, Python will execute all code in the prime.py file, including the print statements. How can we avoid that the print statements are executed? The standard solution in Python for this is to modify the prime.py file as follows:
def prime ( n ): """ Determines whether n is a prime number. This function determines whether the positive integer n is a prime number. Args: n: a positive integer Returns: A boolean indicating whether n is a prime number. """ return True if __name__ == "__main__": for i in range ( 100 ): print ( i, prime ( i ) )
In this code, the code below __name__ == "__main__" is only executed when the code is not imported from another file. This allows a second program to test the functions in the program without executing the code printing statements in the file.
Adding Assertions in Code
As we have seen in the earlier section, the assert statement is very useful to test whether a function has been implemented correctly. However,this is not the only way that assert can be used. Reconsider our implementation of the prime function:
def prime ( n ): """ Determines whether n is a prime number. This function determines whether the positive integer n is a prime number. Args: n: a positive integer Returns: A boolean indicating whether n is a prime number. """ for i in range(2,n): if n % i == 0: return False return True
Note that in the specification we indicated that this function should only be executed on parameters that represent positive integers. While a perfect programmer would hence not use this function in any other context, no programmer is perfect. The incorrect use of a function can sometimes cause bugs that are very hard to track down. To help a programmer, it can be good to check that the function is used correctly. We can use assert here as well:
def prime ( n ): """ Determines whether n is a prime number. This function determines whether the positive integer n is a prime number. Args: n: a positive integer Returns: A boolean indicating whether n is a prime number. """ assert type ( n ) == int and n >= 1, "n should be a positive integer" for i in range(2,n): if n % i == 0: return False return True
With this added line, every time a programmer uses the function with an argument of an incorrect type, or with a smaller than 1, the code will stop and give an error.
In this course, we will not require you to add asserts to all your functions; however, from time to time we will explicitly ask you to do so.
For the example of lists, the full code now becomes:
def zipper ( l1, l2 ): """ Zips two lists, such that elements of l1 and l2 are interleaved. This function zips two given lists l1 and l2 into a new list [l1[0],l2[0],l1[1],l2[1],...,l1[n],l2[n]], where l1 and l2 must be lists of equal length n. For example, zipper ( [1,2], [3,4] ) will return [1,3,2,4]. Args: l1: a list of length n l2: a list of the same length as l1 Returns: A new list with elements [l1[0],l2[0],l1[1],l2[1],...,l1[n],l2[n]] """ assert type ( l1 ) == list and type ( l2 ) == list and len ( l1 ) == len ( l2 ), "l1 and l2 must be two lists of equal length" new_list = [] for i in range ( len ( l1 ) ): new_list.append ( l1[i] ) new_list.append ( l2[i] ) return new_list
Note that the asserts that are added in the code should correspond closely to the information provided in the docstring.
Other Considerations
At this point you may have the impression that adding specifications, tests and asserts is sufficient to write code of good quality. Certainly it helps. However, it is not sufficient. During this course and during your study you will encounter additional approaches for writing code of good quality. We wish to mention a number of recommendations here:
- Make sure that all functions and variables have names that are easy to understand.
- Use a proper layout for your code, including white spaces. The gold standard for this is the so-called PEP 8 [Pep8] specification. It is highly recommended that your code confirms to PEP 8 standards, so click on this link to check its contents.
- Make sure that your functions are not too long, and that each function has a clearly defined task.
- Avoid copy-pasting code: if you need to copy a piece of code, consider whether it would make sense to put that piece of code in a separate function.
References
| [Pep8] | PEP 8 -- Style Guide for Python Code |
Search Algorithms
Source: this section is not based on external sources.
Linear search
As we have seen in the previous section, lists can be used to store collections of data of arbitrary length. Often one is faced with the problem of finding information in a list. Consider the following example. We are given a list of computers in a large IT department:
computer_names = ["apple", "pear", "cherry", "banana", "mango", "grape", "peach"]
(Clearly, this IT department has drawn inspiration from fruit names.)
If a new computer needs to be installed, the IT department needs to check whether a computer with a given name (for instance, "pear" or "orange") already exists. How do we check this? In Python there is an easy answer to this question. We can write code such as this:
if "pear" in computer_names: print ( "Pear exists ") else: print ( "Pear does not exist")
Easy, right?
Actually, not always.
To understand the weaknesses of this code, it is important to have an understanding of algorithms. An algorithm is an unambiguous specification of how to solve a class of problems, such as the problem of finding a name in a list of names. Algorithms for finding elements in lists are often called search algorithms.
How can a computer find a name in a list? The simplest approach is the following:
def linear_search ( name, list_of_names ): for list_name in list_of_names: if name == list_name: return True return False
Underneath, the in statement in Python works similar to the above function. Consequently, this line of code:
if name in list_of_names:
will give you the same result as this code:
if linear_search(list, list_of_names):
What are the drawbacks of the linear_search function (as well as the in statement)? Let us execute our function on some examples to understand this. Let us first consider the example
if linear_search("apple", computer_names):
In this example, our algorithm is very fast. The first name that we will take from the list is apple. We will find out that this name is equal to the name we are looking for. The linear search function will immediately return the value True.
Let us consider a second example.
if linear_search("orange", computer_names):
The situation is very different in this case. Our algorithm will first look at apple; as we are not looking for apples, it will continue with pear, then cherry, ... and so on, till we arrive at the end of the list. The algorithm will then return False.
Hence, in the worst case, our algorithm will need to look at all elements in the list. If our list has only 9 elements, this is not problematic.
However, suppose that we would use this algorithm to search among all names of users on Facebook (2.3 billion in total). In that case the algorithm would take very long. If we would be looking for a name that is not present on Facebook, we would have to retrieve all 2.3 billion names from the list before we can answer True or False!
As in the worst case we would need to look at every element in the list one after the other, this algorithm is known as a linear search algorithm. The number of elements that we look at in the worst case is a linear function of the number of elements in the list.
This raises the question whether we can do better. Fortunately, in some cases we can.
Binary search
Assume that we would have stored our computer names in a sorted order:
sorted_computer_names = ["apple", "banana", "cherry", "grape", "mango", "peach", "pear"]
Note that we can also obtain such a sorted list using the sorted function:
computer_names = ["apple", "pear", "cherry", "banana", "mango", "grape", "peach"] sorted_computer_names = sorted ( computer_names )
On these sorted lists, we can use an approach that is inspired by how we search for words in a dictionary: we start with the middle page of the dictionary, and based on the words at that page, decide where we continue looking in the dictionary. The following code in Python shows this approach:
def binary_search ( name, list_of_names ): first = 0 last = len(list_of_names)-1 found = False while first<=last and not found: middle = (first + last)//2 if list_of_names[middle] == name: found = True else: if name < list_of_names[middle]: last = middle-1 else: first = middle+1 return found
This code is a little bit more complex than the code we have seen till now!
Let's start with a simple case to understand how this code works. Consider binary_search("grape",sorted_computer_names). Before the start of the while loop, the value for last is 6. As 0<6, we calculate the middle next. The outcome of this is 3. This yields the following situation:
first middle last
+-------+--------+--------+-------+-------+-------+------+
| apple | banana | cherry | grape | mango | peach | pear |
+-------+--------+--------+-------+-------+-------+------+
0 1 2 3 4 5 6
We retrieve the 3rd value of sorted_computer_names next, which happens to be equal to grape. At this moment, the code stops and returns True.
Let's continue with a more complex case: binary_search("orange",sorted_computer_names). Similar to the previous case, we first check list_of_names[3]. Again, we are in the following situation:
first middle last
+-------+--------+--------+-------+-------+-------+------+
| apple | banana | cherry | grape | mango | peach | pear |
+-------+--------+--------+-------+-------+-------+------+
0 1 2 3 4 5 6
Here, we determine that "orange" >="grape". We set first=4, giving the following situation:
middle first last
+-------+--------+--------+-------+-------+-------+------+
| apple | banana | cherry | grape | mango | peach | pear |
+-------+--------+--------+-------+-------+-------+------+
0 1 2 3 4 5 6
Basically, the program has decided at this moment that if the word orange is present in the sorted list, it must be at position 4 or higher.
As last is still 6, and 4<=6, the loop continues. We calculate a new middle: (4 + 6) // 2, which yields the value 5. This gives this situation:
first middle last
+-------+--------+--------+-------+-------+-------+------+
| apple | banana | cherry | grape | mango | peach | pear |
+-------+--------+--------+-------+-------+-------+------+
0 1 2 3 4 5 6
The name at position 5 is peach. As "orange"< "peach", the loop continues; we set last = 5-1, as orange must be somewhere before peach in the list:
first middle
last
+-------+--------+--------+-------+-------+-------+------+
| apple | banana | cherry | grape | mango | peach | pear |
+-------+--------+--------+-------+-------+-------+------+
0 1 2 3 4 5 6
As first<=last, we continue:
first
last
middle
+-------+--------+--------+-------+-------+-------+------+
| apple | banana | cherry | grape | mango | peach | pear |
+-------+--------+--------+-------+-------+-------+------+
0 1 2 3 4 5 6
We test whether "mango"=="orange"; as "mango" < "orange" we obtain the following situation:
last first
middle
+-------+--------+--------+-------+-------+-------+------+
| apple | banana | cherry | grape | mango | peach | pear |
+-------+--------+--------+-------+-------+-------+------+
0 1 2 3 4 5 6
In words, the algorithm believes now that if orange is in the list, it must be after mango, at position 5 or higher. As at this moment last<first, the algorithm stops and returns False.
It is instructive to consider the number of elements in the list that the algorithm compared with orange:
grape peach mango
In total, only 3 elements were considered! This is significantly less than in our earlier algorithm.
At this moment, it can be instructive to use the algorithm to search for other elements in the sorted list. You will see that on this list, the binary_search algorithm will never look at more than 3 elements.
One can wonder how many elements would be considered in the worst case for a sorted list of any other length. To understand how we can generalize our results to other lists, let us first consider a list of 15 elements:
first middle last +---+---+---+---+---+---+---+---+---+---+---+----+----+----+----+----+ | | | | | | | | | | | | | | | | | +---+---+---+---+---+---+---+---+---+---+---+----+----+----+----+----+ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
What would our algorithm do in this case? There are three cases:
- We stop, as the element we are looking for is in the middle. Clearly, this is not the worst case.
- We move last to position 7; in this case we are effectively continuing the algorithm on a part of the list having 7 elements.
- We move first to position 9; in this case we are effectively continuing the algorithm on a part of the list having 7 elements as well.
In the last two cases, we know that the worst case is that we are looking at 3 elements. In total, we hence will look at 4 elements in the worst case.
We can continue this argument. On a list of 31 elements, the worst case number of elements considered will be 5. On a list of 63 elements, it will be 6:
7 3 15 4 31 5 63 6 127 7 255 8 ... ... 4294967295 32
In general, the pattern is this: for a list of length
in the worst case k elements are considered.
As a result, if we have more than 4 billion names in a sorted list, we only need to look at 32 of these names in the worst case to determine whether a given name is present in the list!
This is an enormous improvement over the linear search algorithm.
This improvement was the consequence of a careful consideration of two aspects:
- The organisation of data: we did not put the elements in the list in an arbitrary order; the elements had to be sorted.
- The algorithm operating on the data: we tuned our algorithm such that it worked much better for the chosen organisation of the data.
These two aspects are the topics studied in courses on algorithms and data structures. A good understanding of algorithms and data structures can in practice help a lot to develop programs that work efficiently. You will be able to study these topics in more detail in later courses.
Binary Search on Complex Data structures
The code that we saw in the previous section is useful if we want to test that a given element occurs in a sorted list. We can use this two write programs such as
if binary_search ( computer_name, sorted_computer_names ): print ( "Welcome to our system" ) else: print ( "The specified computer does not exist")
In other words, programs in which we only wish to test the presence of a given element.
Often, however, one does not only want to check that a given computer exists, but one also wants to retrieve information associated with the computer, such as its operating system.
Using nested data structures, we could store such associated information in a sorted list as follows:
sorted_computer_names_os = [("apple","MacOS"), ("banana","Linux"), ("cherry","Linux"), \ ("grape", "MacOS"), ("mango", "Windows"), ("peach", "Windows"), \ ("pear", "Linux")]
Hence, our list now consists of tuples, where the first part of the tuple stores the computer name and the second part stores the operating system.
We cannot use our existing binary_search to look for the data associated with a given name. In our binary_search algorithm, we perform a test like
if list_of_names[middle] == name:
If our lists consists of tuples, list_of_names[middle] will be a tuple, such as ("apple","MacOS"). We can only use our current implementation to search for complete tuples such as ("apple", "MacOS").
The following modification does allow us to retrieve associated information:
def binary_search_retrieve ( name, list_of_names ): first = 0 last = len(list_of_names)-1 found = False while first<=last and not found: middle = (first + last)//2 middle_name, middle_info = list_of_names[middle] if middle_name == name: found = True else: if name < middle_name: last = middle-1 else: first = middle+1 if found: return middle_info else: return None
Observe that in this code, we assume that our list now contains tuples, each of which we can unpack. If the element we are looking for exists, we return the associated value; otherwise, we made the choice to return the special value None. We can now write code such as:
if binary_search_retrieve ( computer_name, sorted_computer_names_os ) == "Windows": print ( "Welcome to our system" ) else: print ( "Your machine does not exist or your operating system is not supported")
While in this example, we associated one string with a computer name, nothing limits us to associate more complex information.
sorted_computer_names_os_cc = [("apple",("MacOS","BE")), ("banana",("Linux","BE")), ("cherry",("Linux","FR")), \ ("grape", ("MacOS","FR")), ("mango", ("Windows","NL")), ("peach", ("Windows", "DE")), \ ("pear", ("Linux","DE"))]
We can still use binary_search_retrieve to write programs such as this:
result = binary_search_retrieve ( computer_name, sorted_computer_names_os_cc ) if result is not None: os, country = result print ( "Welcome! Your operating system is " + os + " and your country " + country ) else: print ( "Your computer is not known")
Our binary search algorithm only works for data that is sorted. Assume we are given more complex data. How we can sort this data? Fortunately, the sorted function that we saw earlier, also works on tuples. In this case, it will use a lexicographical order, in which the order between two tuples is determined by the second element in the tuple if the first elements are equal.
>>> unsorted_numbers = [ (3,4), (6,3), (1,2), (3,5), (6,2) ] >>> sorted (unsorted_numbers) [(1, 2), (3, 4), (3, 5), (6, 2), (6, 3)]
Note that the order of information in a tuple is important when using the sort function. If the information is not in the correct order, one solution is to recreate the data in the desired order. For instance, to sort our computer_names on operating system, we can write
>>>> sorted ( [ ((cnoc[1][0], cnoc[1][1]), cnoc[0]) for cnoc in sorted_computer_names_os_cc ] ) [(('Linux', 'BE'), 'banana'), (('Linux', 'DE'), 'pear'), (('Linux', 'FR'), 'cherry'), \ (('MacOS', 'BE'), 'apple'), (('MacOS', 'FR'), 'grape'), (('Windows', 'DE'), 'peach'), \ (('Windows', 'NL'), 'mango')]
Recreating the data just to order it differently may seem a little complex. Furthermore, our indexing (cnoc[1][0]) becomes cumbersome and hard to read. We will see later in the course that there is an alternative solution to this problem.
Corner cases
In our explanation, we made our lives easy by making a number of implicit assumptions:
- Our lists contain every element only once;
- Our lists had lengths 7, 15, 31, ...
It is important to ask yourself what the code would do if these restrictions no longer hold. We will not discuss these questions in detail in this reference. However, as small exercises consider doing the following:
- Apply the binary_search algorithm on a list of a different length.
- Consider modifying the binary_search_retrieve function such that it returns a list of all values associated with a given name.
Glossary
- algorithm
- An unambiguous specification of how to solve a class of problems.
- binary search
- A search algorithm that searches by repeatedly splitting a list in two parts
- linear search
- A search algorithm that considers all elements of a list in the worst case
- search algorithm
- An algorithm for searching an element that fulfills a well-defined set of requirements
Files
Source: this section is based on both [ThinkCS] and [PythonForBeginners].
About files
While a program is running, its data is stored in random access memory (RAM). RAM is fast and inexpensive, but it is also volatile, which means that when the program ends, or the computer shuts down, data in RAM disappears. To make data available the next time the computer is turned on and the program is started, it has to be written to a non-volatile storage medium, such a hard drive, usb drive, or CD-RW.
Data on non-volatile storage media is stored in named locations on the media called files. By reading and writing files, programs can save information between program runs.
Working with files is a lot like working with a notebook. To use a notebook, it has to be opened. When done, it has to be closed. While the notebook is open, it can either be read from or written to. In either case, the notebook holder knows where they are. They can read the whole notebook in its natural order or they can skip around.
All of this applies to files as well. To open a file, we specify its name and indicate whether we want to read or write.
Writing our first file
Let's begin with a simple program that writes four lines of text into a file:
file = open("testfile.txt","w") file.write("Hello World\n") file.write("This is our new text file\n") file.write("and this is another line.\n") file.write("Why? Because we can.\n") file.close()
Opening a file creates what we call a file handle. In this example, the variable file refers to the new handle object. Our program calls methods on the handle, and this makes changes to the actual file which is usually located on our disk.
On line 1, the open function takes two arguments. The first is the name of the file, and the second is the mode. Mode "w" means that we are opening the file for writing.
With mode "w", if there is no file named testfile.txt on the disk, it will be created. If there already is one, it will be replaced by the file we are writing.
To put data in the file we invoke the write method on the handle, shown in lines 2, 3, 4 and 5 above. In bigger programs, lines 2--5 will usually be replaced by a loop that writes many more lines into the file.
Closing the file handle (line 6) tells the system that we are done writing and makes the disk file available for reading by other programs (or by our own program).
A handle is somewhat like a TV remote control
We're all familiar with a remote control for a TV. We perform operations on the remote control --- switch channels, change the volume, etc. But the real action happens on the TV. So, by simple analogy, we'd call the remote control our handle to the underlying TV.
Sometimes we want to emphasize the difference --- the file handle is not the same as the file, and the remote control is not the same as the TV. But at other times we prefer to treat them as a single mental chunk, or abstraction, and we'll just say "close the file", or "flip the TV channel".
Reading a Text File in Python
There are several ways to read a text file in Python. If you just need to extract a string that contains all characters in the file, you can use the following method:
file.read()
For example, the following Python code would print out the file we have just created on the console.
file = open("testfile.txt", "r") print(file.read()) file.close ()
The output of this command will display all the text inside the file, the same text we told the interpreter to add earlier:
Hello World This is our new text file and this is another line. Why? Because we can.
Another way to read a file is to read a certain number of characters. For example, with the following code the Python interpreter will read the first five characters of text from the file and return it as a string:
file = open("testfile.txt", "r") print(file.read(5)) file.close ()
Notice how we’re using the same file.read() method, only this time we specify the number of characters to process. This time the text displayed will be:
Hello
Finally, if you would want to read the file line by line – as opposed to pulling the content of the entire file in a string at once – then you can use the readline() method. Why would you want to use something like this? Let’s say you only want to see the first line of the file – or the third. You would execute the readline() method as many times as possible to get the data you were looking for. Each time you run the method, it will return a string of characters that contains the next line of information from the file. For example:
file = open("testfile.txt", "r") print(file.readline()) print(file.readline()) file.close ()
This command would print the first two lines of the file, like so:
Hello World This is our new text file
Note that an empty line is printed between these two lines. This is because, by default, the print() command always prints a newline after every string. The string that we are printing here, however, ends with a newline itself: this newline was read from the input file, and was not removed by Python.
The additional newline can be avoided using the following approach. We can tell the print command to end the line being printed not by a newline character, for example the empty character '':
file = open("testfile.txt", "r") print(file.readline(),end="") print(file.readline(),end="") file.close ()
Now we get the same result but without empty lines in between:
Hello World This is our new text file
Related to the readline() method is the` readlines() method.
file = open("testfile.txt", "r") print(file.readlines()) file.close ()
The output you would get is a list containing each line as a separate element:
['Hello World\n', 'This is our new text file\n', 'and this is another line.\n', 'Why? Because we can.\n']
Notice how every line is ended with a n, the newline character.
If you would now wish to determine, for example, the third line in the file, we could use the following code (we use the index 2 instead of 3 since the first element of a list is at position 0):
file = open("testfile.txt", "r") print(file.readlines()[2])
which prints:
and this is another line.
Looping over a file object
Using the readlines() notation, we can write code as follows:
file = open("testfile.txt", "r") for line in file.readlines (): print(line,end='') file.close ()
While correct, this code is not very memory efficient. It would read the entire file in a list, and then traverse this list. When you want to read all the lines from a file in a more memory efficient, and fast manner, using a for-loop, Python provides a method that is both simple and easy to read:
file = open("testfile.txt", "r") for line in file: print(line,end='') file.close ()
In this case, Python will avoid loading the entire file in memory. Note how we used the print statement with a second argument again, to avoid having undesired newlines. The code above will print:
Hello World This is our new text file and this is another line. Why? Because we can.
Using the File write method to add
One thing you’ll notice about the file write method is that it only requires a single parameter, which is the string you want to be written. This method can also be used to add information or content to an existing file. You just need to make sure to open the file in append mode "a" to make sure you append, instead of overwriting the existing file.
file = open("testfile.txt", "a") file.write("This is a test\n") file.write("To add more lines.\n") file.close()
This will amend our current file to include the two new lines of text. If you don't believe it, open the changed file in your text editor, or write a Python code fragment to print its current contents.
Closing a File
When you’re done reading or writing a file, it is good practice to call the close() method. By calling this method, you tell the operating system that your program has finished working on the file, and that the file can now be read or written by other programs on your computer. For instance, as long as your program is reading a file, your operating system may decide not to allow other programs to change the file.
While in principle you could keep a file open during the execution of the program, hence, it is a matter of good manners towards other programs to close your files when you don't need access to them any more. For this reason, in our examples we are always closing our files.
It’s important to understand that when you use the close() method, any further attempts to use the file object will fail.
Writing multiple lines at once
You can also use the writelines method to write (or append) multiple lines to a file at once:
file = open("testfile.txt", "a") lines_of_text = ["One line of text here\n", "and another line here\n", "and yet another here\n", "and so on and so forth\n"] file.writelines(lines_of_text) file.close()
Splitting lines in a text file
Methods on strings are very useful when processing files. As a final example, let’s explore how to split a file in the words contained in the file. Using the split method in strings discussed earlier, we can write:
file = open("testfile.txt", “r”): data = file.readlines() for line in data: words = line.split() print(words)
The output for this will be something like (depending on what your testfile currently contains):
['One', 'line', 'of', 'text', 'here'] ['and', 'another', 'line', 'here'] ['and', 'yet', 'another', 'here'] ['and', 'so', 'on', 'and', 'so', 'forth']
The reason the words are presented in this manner is because they are stored – and returned – as a list.
Working with binary files
Files that hold photographs, videos, zip files, executable programs, etc. are called binary files: they're not organized into lines, and cannot be opened with a normal text editor. Python works just as easily with binary files, but when we read from the file we're going to get bytes back rather than a string. Here we'll copy one binary file to another:
f = open("somefile.zip", "rb") g = open("thecopy.zip", "wb") while True: buf = f.read(1024) if len(buf) == 0: break g.write(buf) f.close() g.close()
There are a few new things here. In lines 1 and 2 we added a "b" to the mode to tell Python that the files are binary rather than text files. In line 5, we see read can take an argument which tells it how many bytes to attempt to read from the file. Here we chose to read and write up to 1024 bytes on each iteration of the loop. When we get back an empty buffer from our attempt to read, we know we can break out of the loop and close both the files.
If we set a breakpoint at line 6, (or print type(buf) there) we'll see that the type of buf is bytes. We don't do any detailed work with bytes objects in this textbook.
Directories
Files on non-volatile storage media are organized by a set of rules known as a file system. File systems are made up of files and directories, which are containers for both files and other directories.
When we create a new file by opening it and writing, the new file goes in the current directory (wherever we were when we ran the program). Similarly, when we open a file for reading, Python looks for it in the current directory.
If we want to open a file somewhere else, we have to specify the path to the file, which is the name of the directory (or folder) where the file is located:
>>> wordsfile = open("/usr/share/dict/words", "r") >>> wordlist = wordsfile.readlines() >>> print(wordlist[:6]) ['\n', 'A\n', "A's\n", 'AOL\n', "AOL's\n", 'Aachen\n']
This (Unix) example opens a file named words that resides in a directory named dict, which resides in share, which resides in usr, which resides in the top-level directory of the system, called /. It then reads in each line into a list using readlines, and prints out the first 5 elements from that list.
A Windows path might be "c:/temp/words.txt" or "c:\\temp\\words.txt". Because backslashes are used to escape things like newlines and tabs, we need to write two backslashes in a literal string to get one! So the length of these two strings is the same!
We cannot use / or \ as part of a filename; they are reserved as a delimiter between directory and filenames.
The file /usr/share/dict/words should exist on Unix-based systems, and contains a list of words in alphabetical order.
Glossary
- delimiter
- A sequence of one or more characters used to specify the boundary between separate parts of text.
- directory
- A named collection of files, also called a folder. Directories can contain files and other directories, which are referred to as subdirectories of the directory that contains them.
- file
- A named entity, usually stored on a hard drive, floppy disk, or CD-ROM, that contains a stream of characters.
- file system
- A method for naming, accessing, and organizing files and the data they contain.
- handle
- An object in our program that is connected to an underlying resource (e.g. a file). The file handle lets our program manipulate/read/write/close the actual file that is on our disk.
- mode
- A distinct method of operation within a computer program. Files in Python can be opened in one of four modes: read ("r"), write ("w"), append ("a"), and read and write ("+").
- non-volatile memory
- Memory that can maintain its state without power. Hard drives, flash drives, and rewritable compact disks (CD-RW) are each examples of non-volatile memory.
- path
- A sequence of directory names that specifies the exact location of a file.
- text file
- A file that contains printable characters organized into lines separated by newline characters.
- socket
- One end of a connection allowing one to read and write information to or from another computer.
- volatile memory
- Memory which requires an electrical current to maintain state. The main memory or RAM of a computer is volatile. Information stored in RAM is lost when the computer is turned off.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
| [PythonForBeginners] | https://www.pythonforbeginners.com/files/reading-and-writing-files-in-python |
Exceptions
Source: this section is based on [ThinkCS]
Catching exceptions
Whenever a runtime error occurs, it creates an exception object. The program stops running at this point and Python prints out the traceback, which ends with a message describing the exception that occurred.
For example, dividing by zero creates an exception:
>>> print(55/0) Traceback (most recent call last): File "<interactive input>", line 1, in <module> ZeroDivisionError: integer division or modulo by zero
So does accessing a non-existent list item:
>>> a = [] >>> print(a[5]) Traceback (most recent call last): File "<interactive input>", line 1, in <module> IndexError: list index out of range
Or trying to make an item assignment on a tuple:
>>> tup = ("a", "b", "d", "d") >>> tup[2] = "c" Traceback (most recent call last): File "<interactive input>", line 1, in <module> TypeError: 'tuple' object does not support item assignment
In each case, the error message on the last line has two parts: the type of error before the colon, and specifics about the error after the colon.
Sometimes we want to execute an operation that might cause an exception, but we don't want the program to stop. In this case, we wish to handle the exception.
For example, we might prompt the user for the name of a file and then try to open it. If the file doesn't exist, we don't want the program to crash; we want to handle the exception. We can do this using the try statement to "wrap" a region of code:
filename = input("Enter a file name: ") try: f = open(filename, "r") lines = f.readlines () f.close () except: print("There is no file named", filename)
The try statement has three separate clauses, or parts, introduced by the keywords try ... except ... finally. Either the except or the finally clauses can be omitted, so the above code considers the most common version of the try statement first.
The try statement executes and monitors the statements in the first block. If no exceptions occur, it skips the block under the except clause. If any exception occurs, it executes the statements in the except clause and then continues.
We can use multiple except clauses to handle different kinds of exceptions (see the Errors and Exceptions lesson from Python creator Guido van Rossum's Python Tutorial for a more complete discussion of exceptions). So the program could do one thing if the file does not exist, but do something else if the file was in use by another program.
Raising our own exceptions
Can our program deliberately cause its own exceptions? If our program detects an error condition, we can also raise an exception ourselves. Here is an example that gets input from the user and checks that the number is non-negative:
def get_age(): age = int(input("Please enter your age: ")) if age < 0: # Create a new instance of an exception my_error = ValueError(str(age) + " is not a valid age") raise my_error return age
Line 5 creates an exception object, in this case, a ValueError object, which encapsulates specific information about the error. ValueError is a type of exception that is built into Python and is used by Python in case it encounters a value problem; we can also raise it ourselves.
Python's raise statement is somewhat similar to the return statement: it also returns information to a program that called this function. There are however some important differences between return statements and raise statements. This is illustrated by the following longer program.
def get_age(): age = int(input("Please enter your age: ")) if age < 0: # Create a new instance of an exception my_error = ValueError(str(age) + " is not a valid age") raise my_error return age def contains_digit(s): """ pre: s is a string post: returns True if s contains a digit, and False otherwise """ for l in s: if l in "0123456789": return True return False def get_username(): name = input("Please enter your username: ") if contains_digit(name): my_error = ValueError(name + " is not a valid name") raise my_error return name def get_information (): age = get_age () username = get_username () return ( age, username ) try: age, username = get_information () print ( "Your username is " + username + "; your age is + str(age) ) except: print ( "Error entering information")
Note that in this program, function get_information () does not contain a try ... except block. In this program, the get_information function first calls get_age to ask for an age, and then get_username to ask for a name. What happens if the user does not enter a valid age? In this case, the get_age function raises an exception. However, the execution will not continue in the get_information function. As get_information does not handle exceptions, the program will backtrack towards the main part of the program, which contains a try ... except block. Here, it will not print the Your username is... message, but will rather print the Error entering information message.
Hence, where a return statement in a function will always return to the place where the function was called, a raise statement will break of multiple function calls, till it reaches a place where the exception is handled using a try ... except block. We call this "unwinding the call stack".
ValueError is one of the built-in exception types which most closely matches the kind of error we want to raise. The complete listing of built-in exceptions can be found at the Built-in Exceptions section of the Python Library Reference , again by Python's creator, Guido van Rossum. If Python stops with an error, it also displays the type of the error that caused it to stop.
If we would call the get_age function without try ... except block, we would get this output:
>>> get_age() Please enter your age: 42 42 >>> get_age() Please enter your age: -2 Traceback (most recent call last): File "<interactive input>", line 1, in <module> File "learn_exceptions.py", line 4, in get_age raise ValueError(str(age)+ " is not a valid age") ValueError: -2 is not a valid age
The error message includes the exception type and the additional information that was provided when the exception object was first created.
We can also print the more specific error message using this code:
try: age, username = get_information () print ( "Your username is " + username + " your age is " + str(age)) except ValueError as error: print ( error )
In this case, the try ... except block will only catch an exception of the type ValueError. It will store information regarding this exception, as created by raise statement in the error value, which we can subsequently print.
With statement
As pointed out earlier, a common situation in which exceptions are useful, is when working with files. We saw this code earlier:
filename = input("Enter a file name: ") try: f = open(filename, "r") lines = f.readlines () f.close () except: print("There is no file named", filename)
In this example, the program will print the message There is no file ... when the file does not exist.
Let us now consider this variation, in which we use the get_name function of the previous section:
filename = input("Enter a file name: ") try: f = open(filename, "r") username = get_username () for line in f: if line == username: print ( username + " found!" ) f.close () except IOError: print("There is no file named", filename) except ValueError: print("Incorrect name provided")
In this code, two different exceptions can occur: one is related to a file error, the other to the provision of an incorrect name. These two types of errors are distinguished by having two except statements; each of these will catch the corresponding type of error.
Many tricky things are happening in this code: we have one try ... except block for different types of errors, depending on whether or not the file exists we will ask for a name, and so on. One thing is happening in this code that makes it particularly undesirable. As stated earlier, it is considered good practice for a program to close every file that it opens.
In the program above, if an incorrect username is entered, the program will raise an exception, and jump towards printing the message Incorrect name provided without executing the close() instruction: after all, the close() statement is only executed after we have successfully finished the get_username() function.
To resolve this issue, the proper way to combine exception handling with file processing is as follows:
filename = input("Enter a file name: ") try: with open(filename, "r") as f: username = get_username () for line in f: if line == username: print ( "{0} found!".format ( username ) ) except IOError: print("There is no file named", filename) except ValueError: print("Incorrect name provided")
In this code there is no close() statement any more! Instead, we have used the with open(filename, "r") as f: construction. What does this construction do? Essentially, it associates the result of open(filename, "r") to f, and executes the block of code
username = get_username () for line in f: if line == username: print ( "{0} found!".format ( username ) )
if the file was opened successfully. Two things can then happen:
- the code executes successfully; in this case, the file will be closed automatically when the code is finished.
- the code raises an execption; in this case, the file will be closed before the execution is passed on to the exception handler.
Hence, the with statement can be used to ensure that a file is automatically closed in all circumstances, whether good or bad.
Many Python programmers nowadays use with every time they open a file, as by using this statement, one does not need to think about closing a file any more: it will always happen after the specified piece of code is finished.
Let’s take a look at another example, which prints all the data in a file, line by line:
with open("testfile.txt") as file: data = file.readlines() for line in data: print(line, end='')
Notice that in the above example we didn’t use the file.close() method because the with statement will automatically call that for us upon execution. It really makes things a lot easier, doesn’t it?
Glossary
- exception
- An error that occurs at runtime.
- handle an exception
- To prevent an exception from causing our program to crash, by wrapping the block of code in a try ... except construct.
- raise
- To create a deliberate exception by using the raise statement.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Dictionaries
Source: this section is heavily based on [ThinkCS].
All of the compound data types we have studied in detail so far --- strings, lists, and tuples --- are sequence types, which use integers as indices to access the values they contain within them.
Dictionaries are yet another kind of compound type. They are Python's built-in mapping type. They map keys, which can be any immutable type, to values, which can be any type (heterogeneous), just like the elements of a list or tuple. In other languages, they are called associative arrays since they associate a key with a value.
As an example, we will create a dictionary to translate English words into Spanish. For this dictionary, the keys are strings.
One way to create a dictionary is to start with the empty dictionary and add key:value pairs. The empty dictionary is denoted {}:
>>> eng2sp = {} >>> eng2sp["one"] = "uno" >>> eng2sp["two"] = "dos"
The first assignment creates a dictionary named eng2sp; the other assignments add new key:value pairs to the dictionary. We can print the current value of the dictionary in the usual way:
>>> print(eng2sp) {"two": "dos", "one": "uno"}
The key:value pairs of the dictionary are separated by commas. Each pair contains a key and a value separated by a colon.
Hashing
The order of the pairs may not be what was expected. Python uses complex algorithms, designed for very fast access, to determine where the key:value pairs are stored in a dictionary. For our purposes we can think of this ordering as unpredictable.
You also might wonder why we use dictionaries at all when the same concept of mapping a key to a value could be implemented using a list of tuples:
>>> {"apples": 430, "bananas": 312, "oranges": 525, "pears": 217} {'pears': 217, 'apples': 430, 'oranges': 525, 'bananas': 312} >>> [('apples', 430), ('bananas', 312), ('oranges', 525), ('pears', 217)] [('apples', 430), ('bananas', 312), ('oranges', 525), ('pears', 217)]
The reason is dictionaries are very fast, both to update and to search, implemented using a technique called hashing, which allows us to access a value very quickly, and to remove and add values quickly. By contrast, the list of tuples implementation is slow, either to update, or to search into. If we wanted to find a value associated with a key in an unordered list, we would have to iterate over every tuple. What if the key wasn't even in the list? We would have to get to the end of it to find out. If we wanted to add a value with a key in an ordered list, we would have to move all elements in the list if we need to put the new value at the beginning of the list.
Another way to create a dictionary is to provide a list of key:value pairs using the same syntax as the previous output:
>>> eng2sp = {"one": "uno", "two": "dos", "three": "tres"}
It doesn't matter what order we write the pairs. The values in a dictionary are accessed with keys, not with indices, so there is no need to care about ordering.
Here is how we use a key to look up the corresponding value:
>>> print(eng2sp["two"]) 'dos'
The key "two" yields the value "dos".
Lists, tuples, and strings have been called sequences, because their items occur in order. The dictionary is the first compound type that we've seen that is not a sequence, so we can't index or slice a dictionary.
Dictionary operations
The del statement removes a key:value pair from a dictionary. For example, the following dictionary contains the names of various fruits and the number of each fruit in stock:
>>> inventory = {"apples": 430, "bananas": 312, "oranges": 525, "pears": 217} >>> print(inventory) {'pears': 217, 'apples': 430, 'oranges': 525, 'bananas': 312}
If someone buys all of the pears, we can remove the entry from the dictionary:
>>> del inventory["pears"] >>> print(inventory) {'apples': 430, 'oranges': 525, 'bananas': 312}
Or if we're expecting more pears soon, we might just change the value associated with pears:
>>> inventory["pears"] = 0 >>> print(inventory) {'pears': 0, 'apples': 430, 'oranges': 525, 'bananas': 312}
A new shipment of bananas arriving could be handled like this:
>>> inventory["bananas"] += 200 >>> print(inventory) {'pears': 0, 'apples': 430, 'oranges': 525, 'bananas': 512}
The len function also works on dictionaries; it returns the number of key:value pairs:
>>> len(inventory) 4
Dictionary methods
Dictionaries have a number of useful built-in methods.
The keys method returns what Python 3 calls a view of its underlying keys. A view object has some similarities to the range object we saw earlier --- it is a lazy promise, to deliver its elements when they're needed by the rest of the program. We can iterate over the view, or turn the view into a list like this:
for k in eng2sp.keys(): # The order of the k's is not defined print("Got key", k, "which maps to value", eng2sp[k]) ks = list(eng2sp.keys()) print(ks)
This produces this output:
Got key three which maps to value tres Got key two which maps to value dos Got key one which maps to value uno ['three', 'two', 'one']
It is so common to iterate over the keys in a dictionary that we can omit the keys method call in the for loop --- iterating over a dictionary implicitly iterates over its keys:
for k in eng2sp: print("Got key", k)
The values method is similar; it returns a view object which can be turned into a list:
>>> list(eng2sp.values()) ['tres', 'dos', 'uno']
The items method also returns a view, which promises a list of tuples --- one tuple for each key:value pair:
>>> list(eng2sp.items()) [('three', 'tres'), ('two', 'dos'), ('one', 'uno')]
Tuples are often useful for getting both the key and the value at the same time while we are looping:
for (k,v) in eng2sp.items(): print("Got",k,"that maps to",v)
This produces:
Got three that maps to tres Got two that maps to dos Got one that maps to uno
The in and not in operators can test if a key is in the dictionary:
>>> "one" in eng2sp True >>> "six" in eng2sp False >>> "tres" in eng2sp # Note that 'in' tests keys, not values. False
This method can be very useful, since looking up a non-existent key in a dictionary causes a runtime error:
>>> eng2esp["dog"] Traceback (most recent call last): ... KeyError: 'dog'
Aliasing and copying
As in the case of lists, because dictionaries are mutable, we need to be aware of aliasing. Whenever two variables refer to the same object, changes to one affect the other.
If we want to modify a dictionary and keep a copy of the original, use the copy method. For example, opposites is a dictionary that contains pairs of opposites:
>>> opposites = {"up": "down", "right": "wrong", "yes": "no"} >>> alias = opposites >>> copy = opposites.copy() # Shallow copy
alias and opposites refer to the same object; copy refers to a fresh copy of the same dictionary. If we modify alias, opposites is also changed:
>>> alias["right"] = "left" >>> opposites["right"] 'left'
If we modify copy, opposites is unchanged:
>>> copy["right"] = "privilege" >>> opposites["right"] 'left'
Sparse matrices
We previously used a list of lists to represent a matrix. That is a good choice for a matrix with mostly nonzero values, but consider a sparse matrix like this one:
The list representation contains a lot of zeroes:
matrix = [[0, 0, 0, 1, 0], [0, 0, 0, 0, 0], [0, 2, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 3, 0]]
An alternative is to use a dictionary. For the keys, we can use tuples that contain the row and column numbers. Here is the dictionary representation of the same matrix:
>>> matrix = {(0, 3): 1, (2, 1): 2, (4, 3): 3}
We only need three key:value pairs, one for each nonzero element of the matrix. Each key is a tuple, and each value is an integer.
To access an element of the matrix, we could use the [] operator:
>>> matrix[(0, 3)] 1
Notice that the syntax for the dictionary representation is not the same as the syntax for the nested list representation. Instead of two integer indices, we use one index, which is a tuple of integers.
There is one problem. If we specify an element that is zero, we get an error, because there is no entry in the dictionary with that key:
>>> matrix[(1, 3)] KeyError: (1, 3)
The get method solves this problem:
>>> matrix.get((0, 3), 0) 1
The first argument is the key; the second argument is the value get should return if the key is not in the dictionary:
>>> matrix.get((1, 3), 0) 0
get definitely improves the semantics of accessing a sparse matrix. Shame about the syntax.
Counting letters
In the exercises in Strings we wrote a function that counted the number of occurrences of a letter in a string. A more general version of this problem is to form a frequency table of the letters in the string, that is, how many times each letter appears.
Such a frequency table might be useful for compressing a text file. Because different letters appear with different frequencies, we can compress a file by using shorter codes for common letters and longer codes for letters that appear less frequently.
Dictionaries provide an elegant way to generate a frequency table:
>>> letter_counts = {} >>> for letter in "Mississippi": ... letter_counts[letter] = letter_counts.get(letter, 0) + 1 ... >>> letter_counts {'M': 1, 's': 4, 'p': 2, 'i': 4}
We start with an empty dictionary. For each letter in the string, we find the current count (possibly zero) and increment it. At the end, the dictionary contains pairs of letters and their frequencies.
It might be more appealing to display the frequency table in alphabetical order. We can do that with the items and sort methods:
>>> letter_items = list(letter_counts.items()) >>> letter_items.sort() >>> print(letter_items) [('M', 1), ('i', 4), ('p', 2), ('s', 4)]
Notice in the first line we had to call the type conversion function list. That turns the promise we get from items into a list, a step that is needed before we can use the list's sort method.
Glossary
- call graph
- A graph consisting of nodes which represent function frames (or invocations), and directed edges (lines with arrows) showing which frames gave rise to other frames.
- dictionary
- A collection of key:value pairs that maps from keys to values. The keys can be any immutable value, and the associated value can be of any type.
- immutable data value
- A data value which cannot be modified. Assignments to elements or slices (sub-parts) of immutable values cause a runtime error.
- key
- A data item that is mapped to a value in a dictionary. Keys are used to look up values in a dictionary. Each key must be unique across the dictionary.
- key:value pair
- One of the pairs of items in a dictionary. Values are looked up in a dictionary by key.
- mapping type
- A mapping type is a data type comprised of a collection of keys and associated values. Python's only built-in mapping type is the dictionary. Dictionaries implement the associative array abstract data type.
- mutable data value
- A data value which can be modified. The types of all mutable values are compound types. Lists and dictionaries are mutable; strings and tuples are not.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |