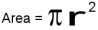Type converter functions

As indicated earlier, the information that a variable refers to has both a type and a value. Sometimes it is useful to change the value from one type to another. Here we'll look at three more Python functions, int, float and str, which will (attempt to) convert their arguments into types int, float and str respectively. We call these type converter functions.

The int function can take a floating point number or a string, and turn it into an int. For floating point numbers, it discards the decimal portion of the number --- a process we call truncation towards zero on the number line. Let us see this in action:

>>> int(3.14)
3
>>> int(3.9999)             # This doesn't round to the closest int!
3
>>> int(3.0)
3
>>> int(-3.999)             # Note that the result is closer to zero
-3
>>> int(minutes / 60)
10
>>> int("2345")             # Parse a string to produce an int
2345
>>> int(17)                 # It even works if arg is already an int
17
>>> int("23 bottles")

This last case doesn't look like a number --- what do we expect?

Traceback (most recent call last):
File "<interactive input>", line 1, in <module>
ValueError: invalid literal for int() with base 10: '23 bottles'

The type converter float can turn an integer, a float, or a syntactically legal string into a float:

>>> float(17)
17.0
>>> float("123.45")
123.45

The type converter str turns its argument into a string:

>>> str(17)
'17'
>>> str(123.45)
'123.45'

Operations on strings

In general, you cannot perform mathematical operations on strings, even if the strings look like numbers. The following are illegal (assuming that message has type string):

>>> message - 1        # Error
>>> "Hello" / 123      # Error
>>> message * "Hello"  # Error
>>> "15" + 2           # Error

Interestingly, the + operator does work with strings, but for strings, the + operator represents concatenation, not addition. Concatenation means joining the two operands by linking them end-to-end. For example:

fruit = "banana"
baked_good = " nut bread"
print(fruit + baked_good)

The output of this program is banana nut bread. The space before the word nut is part of the string, and is necessary to produce the space between the concatenated strings.

The * operator also works on strings; it performs repetition. For example, 'Fun'*3 is 'FunFunFun'. One of the operands has to be a string; the other has to be an integer.

On one hand, this interpretation of + and * makes sense by analogy with addition and multiplication. Just as 4*3 is equivalent to 4+4+4, we expect "Fun"*3 to be the same as "Fun"+"Fun"+"Fun", and it is. On the other hand, there is a significant way in which string concatenation and repetition are different from integer addition and multiplication. Can you think of a property that addition and multiplication have that string concatenation and repetition do not?

Input

There is a built-in function in Python for getting input from the user:

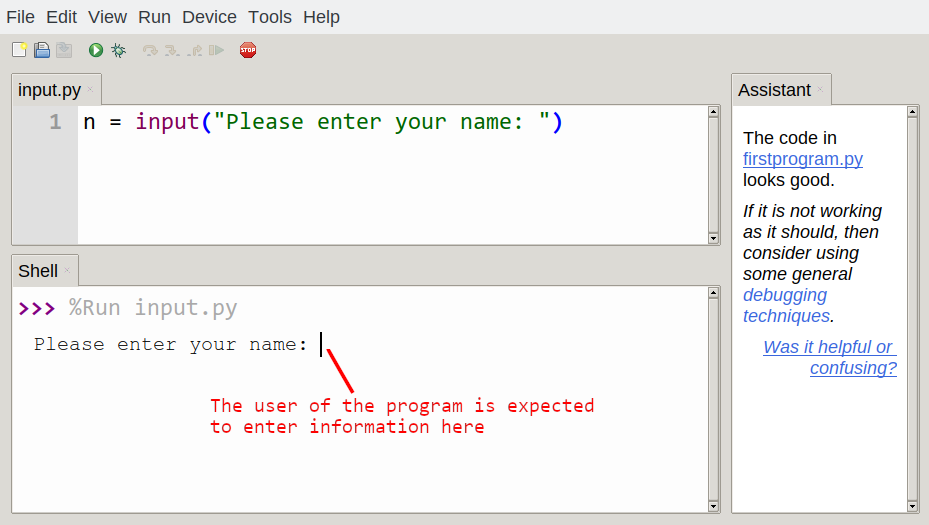
n = input("Please enter your name: ")

A sample run of this script in Thonny would look like this:

The user of the program can enter the name and press enter, and when this happens the text that has been entered is returned from the input function, and in this case assigned to the variable n.

Even if you asked the user to enter their age, you would get back a string like "17". It would be your job, as the programmer, to convert that string into a int or a float, using the int or float converter functions we saw earlier.

Composition

One of the most useful features of programming languages is their ability to take small building blocks and compose them into larger chunks.

For example, we know how to get the user to enter some input, we know how to convert the string we get into a float, we know how to write a complex expression, and we know how to print values. Let's put these together in a small four-step program that asks the user to input a value for the radius of a circle, and then computes the area of the circle from the formula.

Firstly, we'll do the four steps one at a time:

response = input("What is your radius? ")
r = float(response)
area = 3.14159 * r**2
print("The area is ", area)

Now let's compose the first two lines into a single line of code, and compose the second two lines into another line of code.

r = float( input("What is your radius? ") )
print("The area is ", 3.14159 * r**2)

If we really wanted to be tricky, we could write it all in one statement:

print("The area is ", 3.14159*float(input("What is your radius?"))**2)

Such compact code may not be most understandable for humans, but it does illustrate how we can compose bigger chunks from our building blocks.

If you're ever in doubt about whether to compose code or fragment it into smaller steps, try to make it as simple as you can for the human to follow. My choice would be the first case above, with four separate steps.

The modulus operator

The modulus operator works on integers (and integer expressions) and gives the remainder when the first number is divided by the second. In Python, the modulus operator is a percent sign (%). The syntax is the same as for other operators. It has the same precedence as the multiplication operator.

>>> q = 7 // 3     # This is integer division operator
>>> print(q)
2
>>> r  = 7 % 3
>>> print(r)
1

So 7 divided by 3 is 2 with a remainder of 1.

The modulus operator turns out to be surprisingly useful in larger programs. For example, you can check whether one number is divisible by another---if x % y is zero, then x is divisible by y.

Also, you can extract the right-most digit or digits from a number. For example, x % 10 yields the right-most digit of x (in base 10). Similarly x % 100 yields the last two digits.

It is also extremely useful for doing conversions, say from seconds, to hours, minutes and seconds. So let's write a program to ask the user to enter some seconds, and we'll convert them into hours, minutes, and remaining seconds.

total_secs = int(input("How many seconds, in total?"))
hours = total_secs // 3600
secs_still_remaining = total_secs % 3600
minutes =  secs_still_remaining // 60
secs_finally_remaining = secs_still_remaining  % 60

print("Hrs=", hours, "  mins=", minutes,
                         "secs=", secs_finally_remaining)

Chained conditionals

We have now seen how to combine types and expressions in more complex statements. Similarly, we can also combine if statements in more complex manners. The basic if statement had two branches. Sometimes there are more than two possibilities and we need more than two branches. One way to express a computation like that is a chained conditional:

if x < y:
    STATEMENTS_A
elif x > y:
    STATEMENTS_B
else:
    STATEMENTS_C

Flowchart of this chained conditional

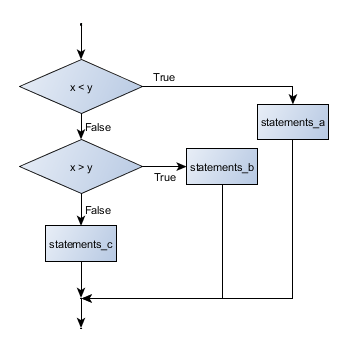
elif is an abbreviation of else if. Again, exactly one branch will be executed. There is no limit of the number of elif statements but only a single (and optional) final else statement is allowed and it must be the last branch in the statement:

if choice == "a":
    function_one()
elif choice == "b":
    function_two()
elif choice == "c":
    function_three()
else:
    print("Invalid choice.")

Each condition is checked in order. If the first is false, the next is checked, and so on. If one of them is true, the corresponding branch executes, and the statement ends. Even if more than one condition is true, only the first true branch executes.

Nested conditionals

One conditional can also be nested within another. (It is the same theme of composability, again!) We could have written the previous example as follows:

Flowchart of this nested conditional

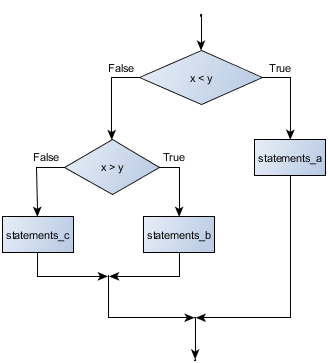
if x < y:
    STATEMENTS_A
else:
    if x > y:
        STATEMENTS_B
    else:
        STATEMENTS_C

The outer conditional contains two branches. The second branch contains another if statement, which has two branches of its own. Those two branches could contain conditional statements as well.

Although the indentation of the statements makes the structure apparent, nested conditionals very quickly become difficult to read. In general, it is a good idea to avoid them when we can.

Logical operators often provide a way to simplify nested conditional statements. For example, we can rewrite the following code using a single conditional:

if 0 < x:            # Assume x is an int here
    if x < 10:
        print("x is a positive single digit.")

The print function is called only if we make it past both the conditionals, so instead of the above which uses two if statements each with a simple condition, we could make a more complex condition using the and operator. Now we only need a single if statement:

if 0 < x and x < 10:
    print("x is a positive single digit.")

Nesting loops and conditionals

Now we have seen that if``s can be nested in each other, it should not come as a surprise that also ``while and if can be nested in each other. Consider the following program:

x = int(input("Provide a number: "))
while x != 0:
    if x < 0:
        print ( -x )
    else:
        print ( x )
    x = int(input("Provide another number: "))

In this code, we continue to ask the user for a number, as long as the user does not enter the number 0. For each such number, we check whether it is positive or negative, and adapt our printing process to the situation. It is perfectly possible to nest the if condition within the while loop.

Also the reverse type of nesting is possible, where we put a while loop within an if block.

Logical opposites

We have already seen how to combine Boolean expressions using and, or and not. Combinations of such expressions can quickly become complex. It is important to then reflect on whether it is possible to simplify such expressions.

Each of the six relational operators has a logical opposite: for example, suppose we can get a driving licence when our age is greater or equal to 17, we can not get the driving licence when we are less than 17.

Notice that the opposite of >= is <.

operator	logical opposite
==	!=
!=	==
<	>=
<=	>
>	<=
>=	<

Understanding these logical opposites allows us to sometimes get rid of not operators. not operators are often quite difficult to read in computer code, and our intentions will usually be clearer if we can eliminate them.

For example, if we wrote this Python:

if not (age >= 17):
    print("Hey, you're too young to get a driving licence!")

it would probably be clearer to use the simplification laws, and to write instead:

if age < 17:
    print("Hey, you're too young to get a driving licence!")

Two powerful simplification laws (called de Morgan's laws) that are often helpful when dealing with complicated Boolean expressions are:

not (x and y)  ==  (not x) or (not y)
not (x or y)   ==  (not x) and (not y)

For example, suppose we can slay the dragon only if our magic lightsabre sword is charged to 90% or higher, and we have 100 or more energy units in our protective shield. We find this fragment of Python code in the game:

if not ((sword_charge >= 0.90) and (shield_energy >= 100)):
    print("Your attack has no effect, the dragon fries you to a crisp!")
else:
    print("The dragon crumples in a heap. You rescue the gorgeous princess!")

de Morgan's laws together with the logical opposites would let us rework the condition in a (perhaps) easier to understand way like this:

if (sword_charge < 0.90) or (shield_energy < 100):
    print("Your attack has no effect, the dragon fries you to a crisp!")
else:
    print("The dragon crumples in a heap. You rescue the gorgeous princess!")

We could also get rid of the not by swapping around the then and else parts of the conditional. So here is a third version, also equivalent:

if (sword_charge >= 0.90) and (shield_energy >= 100):
    print("The dragon crumples in a heap. You rescue the gorgeous princess!")
else:
    print("Your attack has no effect, the dragon fries you to a crisp!")

This version is probably the best of the three, because it very closely matches the initial English statement. Clarity of our code (for other humans), and making it easy to see that the code does what was expected should always be a high priority.

As our programming skills develop we'll find we have more than one way to solve any problem. So good programs are designed. We make choices that favour clarity, simplicity, and elegance. The job title software architect says a lot about what we do --- we are architects who engineer our products to balance beauty, functionality, simplicity and clarity in our creations.

Type conversion

We've had a first look at this earlier in this chapter. Seeing it again won't hurt!

Many Python types come with a built-in function that attempts to convert values of another type into its own type. The int function, for example, takes any value and converts it to an integer, if possible, or complains otherwise:

>>> int("32")
32
>>> int("Hello")
ValueError: invalid literal for int() with base 10: 'Hello'

int can also convert floating-point values to integers, but remember that it truncates the fractional part:

>>> int(-2.3)
-2
>>> int(3.99999)
3
>>> int("42")
42
>>> int(1.0)
1

The float function converts integers and strings to floating-point numbers:

>>> float(32)
32.0
>>> float("3.14159")
3.14159
>>> float(1)
1.0

It may seem odd that Python distinguishes the integer value 1 from the floating-point value 1.0. They may represent the same number, but they belong to different types. The reason is that they are represented differently inside the computer.

The str function converts any argument given to it to type string:

>>> str(32)
'32'
>>> str(3.14149)
'3.14149'
>>> str(True)
'True'
>>> str(true)
Traceback (most recent call last):
  File "<interactive input>", line 1, in <module>
NameError: name 'true' is not defined

str will work with any value and convert it into a string. As mentioned earlier, True is Boolean value; true is just an ordinary variable name, and is not defined here, so we get an error.

Glossary

chained conditional

A conditional branch with more than two possible flows of execution. In Python chained conditionals are written with if ... elif ... else statements.

composition

The ability to combine simple expressions and statements into compound statements and expressions in order to represent complex computations concisely.

concatenate

To join two strings end-to-end.

modulus operator

An operator, denoted with a percent sign ( %), that works on integers and yields the remainder when one number is divided by another.

References