Rectangles

Suppose we want a class to represent rectangles located somewhere in the Cartesian X-Y plane. What information do we have to provide in order to specify such a rectangle? To simplify things, let us assume that the rectangle is always oriented either vertically or horizontally, never at an angle.

There are a few possibilities: we could specify the center of the rectangle (two coordinates) and its size (width and height); or we could specify one of the corners and the size; or we could specify two opposing corners. A conventional choice is to specify the upper-left corner of the rectangle, and its size.

As with the Point class before, we'll define a new class Rectangle, and provide it with an initialiser method __init__ and a string converter method __str__. Also don't forget to always add as first parameter to your methods a reference to self.

class Rectangle:
    """ The Rectangle class represents rectangles in a Cartesian plane. """

    def __init__(self, pos, w, h):
        """ Create a new rectangle with upper-left corner at point pos,
            with width w and height h.
        @pre:  pos is an instance of class Point
               width and height are positive numbers
        @post: the attributes corner, width and height of this rectangle
               instance have been initialised to the values pos, w and h
               passed as arguments
        """
        self.corner = pos
        self.width = w
        self.height = h

    def __str__(self):
        """
        @pre:  -
        @post: returns a string representation of this rectangle in the
               following format ((x, y), width, height) where width and
               height are the values of the corresponding attributes of
               this object and x and y are the corresponding attributes
               of the point object stored in the corner attribute
        """
        return "({0}, {1}, {2})".format(self.corner, self.width, self.height)

box = Rectangle(Point(0, 0), 100, 200)
bomb = Rectangle(Point(100, 80), 5, 10)    # In some video game
print("box: ", box)
print("bomb: ", bomb)

Note how, to specify the upper-left corner, we embedded a Point object (as was defined in the previous section) within our new Rectangle object. We create two new Rectangle objects, and then print them, which produces:

box: ((0, 0), 100, 200)
bomb: ((100, 80), 5, 10)

The dot operator can be composed (chained). For example, the expression box.corner.x means: "Go to the object that box refers to, select its attribute named corner, then go to that object and select its attribute named x".

The figure below shows the state of this object:

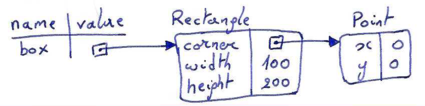
From the figure it can easily be seen that printing box.corner.x would produce:

>>> print(box.corner.x)
0

When reasoning about the state of objects (their attributes and the values they contain), we strongly encourage you to draw such memory diagrams.

Objects are mutable

We can change the state of an object by making an assignment to one of its attributes. For example, to grow the size of a rectangle without changing its position, we could modify the values of its width and height attributes:

box.width += 50
box.height += 100

The memory diagram below sketches the effect of making these modifications (in green):

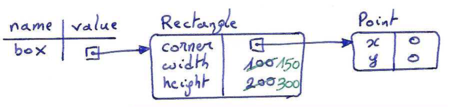
After this, print("box: ", box) produces as output:

box: ((0, 0), 150, 300)

However, we prefer to provide a method to encapsulate this state change operation inside the class. We will also provide another method to move the position of the rectangle over a certain distance:

class Rectangle:
    # ... same as before ...

    def grow(self, delta_width, delta_height):
        """ Grow (or shrink) this rectangle by the deltas
        @pre:  delta_width and delta_height are (positive or negative) numbers
        @post: this rectangle's width was grown to its original width plus
               delta_width (or shrunk in case delta_width is negative);
               this rectangle's height was grown to its original height plus
               delta_height (or shrunk in case delta_height is negative);
               nothing is returned
        """
        self.width += delta_width
        self.height += delta_height

    def move(self, dx, dy):
        """ Move this object by the given distances
        @pre:  dx and dy are (positive or negative) numbers
        @post: the x-coordinate of this rectangle's corner was moved from
               its original position x to x plus dx (moved right if
               dx is positive or moved left if dx is negative);
               the y-coordinate of this rectangle's corner was moved from
               its original position y to y plus dy (moved down if
               dy is positive or moved up if dy is negative);
               nothing is returned
        """
        self.corner.x += dx
        self.corner.y += dy

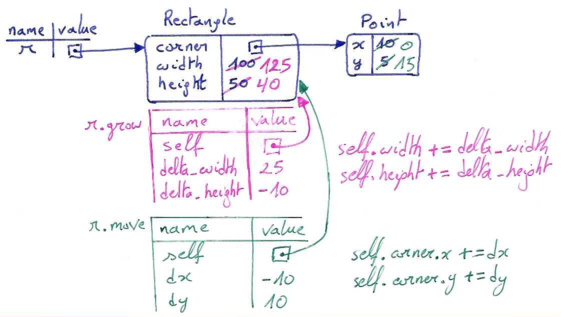
Let us try this:

>>> r = Rectangle(Point(10,5), 100, 50)
>>> print(r)
((10, 5), 100, 50)
>>> r.grow(25, -10)
>>> print(r)
((10, 5), 125, 40)
>>> r.move(-10, 10)
print(r)
((0, 15), 125, 40)

Again, a memory diagram may help you to better visualise how the state of the rectangle and point objects get modified (the part in blue corresponds to the definition of the rectangle object, in pink the effect of growing it, in green the effect of moving it):

Sameness

The meaning of the word "same" seems perfectly clear until we give it some thought, and then we realize there is more to it than we initially expected.

For example, if we say, "Alice and Bob have the same mother", we mean that her mother and his are the same person. If we say, however, "Alice and Bob have the same car", we probably mean that her car and his are the same make and model, but that they are two different cars. But if we say, "Alice and Bob share the same car", we probably mean that they actually share the usage of a single car.

When we talk about objects, there is a similar ambiguity. For example, if two Points are the same, does that mean they are two point objects that contain the same data (coordinates) or that they are actually the same object?

We can use the is operator to find out if two references refer to the same object:

>>> p1 = Point(3, 4)
>>> p2 = Point(3, 4)
>>> p1 is p2
False

In this example, even though p1 and p2 contain the same coordinates, they are not the same object. If we assign the value of p1 to a new variable named p3, however, then the two variables are aliases of (refer to) the same object:

>>> p3 = p1
>>> p1 is p3
True

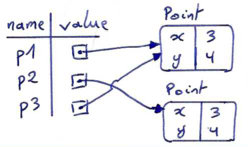
This type of equality is called shallow equality because it compares only the references, not the actual contents of the objects' attributes. With the is operator, two things are considered the same only if they refer to the exact same thing. This means that even the following comparison would yield False:

>>> Point(3, 4) is Point(3, 4)
False

The reason is that whenever you call the Point(3, 4) constructor you create a new distinct point object that happens to have the values 3 and 4 for its x and y coordinates. But the two objects are distinct and stored in different memory locations.

To compare the contents of the objects — deep equality — we can write a function called same_coordinates:

def same_coordinates(p1, p2):
    """
    @pre:  p1 and p2 are instances of class Point
    @post: returns True if both the x attribute of p1 and p2 are equal
           and their y attributes are equal;
           returns False otherwise
    """
    return (p1.x == p2.x) and (p1.y == p2.y)

Now if we try to run the comparisons above again, but using same_coordinates as a comparator rather than the is operator, we can see that they are all considered the same:

>>> same_coordinates(p1, p2)
True
>>> same_coordinates(p1, p3)
True
>>> same_coordinates(Point(3, 4),Point(3, 4))
True

Of course, if two variables refer to the same object (as is the case with p1 and p3), they have both shallow and deep equality.

p1 = Point(4, 2)
p2 = Point(4, 2)
print("== on Points returns", p1 == p2)
# By default, == on Point objects does a SHALLOW equality test

l1 = [2,3]
l2 = [2,3]
print("== on lists returns",  l1 == l2)
# But by default, == does a DEEP equality test on lists

== on Points returns False
== on lists returns True

Copying

Aliasing (different variables referring to a same object) can make a program difficult to read because changes made in one place might have unexpected effects in another place. It is hard to keep track of all the variables that might refer to a given object.

Copying an object is often an alternative to aliasing. The copy module contains a function called copy that can duplicate any object:

>>> import copy
>>> p1 = Point(3, 4)
>>> p2 = copy.copy(p1)
>>> p1 is p2
False
>>> same_coordinates(p1, p2)
True

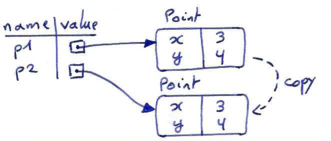
Once we import the copy module, we can use the copy function to make a new Point. p1 and p2 are not a reference to the same object, but they are distinct point objects that contain the same data. p2 is a newly created object of which the data is copied from p1.

To copy a simple object like a Point, which doesn't contain any embedded objects, using the copy function suffices, even though it only performs a shallow copying.

For something like a Rectangle object, which contains an internal reference to a Point object (to represent its upper-left corner), a simple shallow copy wouldn't suffice however. It would create a new Rectangle object, copying the values of the width and height attributes of the original Rectangle object. But for the corner attribute it would simply copy the reference to the Point object it contains, so that both the old and the new Rectangle's corner attribute would refer to the same Point.

>>> import copy
>>> b1 = Rectangle(Point(0, 0), 100, 200)
>>> b2 = copy.copy(b1)

If we create a rectangle b1 in the usual way, and then make a copy b2, using copy, the resulting memory diagram looks like this:

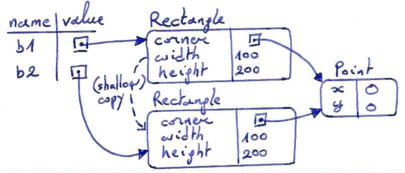
This is almost certainly not what we want. In this case, invoking grow on one of the Rectangle objects would not affect the other (since the grow method only acts on the width and height attributes which were copied), but invoking move on either Rectangle object would affect the other! That would be very weird, since the rectangles would share their upper-left corner but not their size attributes.

>>> b1.move(10,10)
>>> print(b2.corner)
(10,10)

In the example above, although we didn't explicitly move b2, we can see that its corner object has changed as a side-effect of moving b1. This behavior is confusing and error-prone. The problem is that the shallow copy of the rectangle object has created an alias to the Point that represents the corner, rather than making a copy of that point.

Fortunately, the copy module also contains a function named deepcopy that copies not only the object but also any embedded objects (recursively). It won't be surprising to learn that this operation is called a deep copy.

>>> b1 = Rectangle(Point(0, 0), 100, 200)
>>> b2 = copy.deepcopy(b1)
>>> b1.move(10,10)
>>> print(b1.corner)
(10,10)
>>> print(b2.corner)
(0,0)

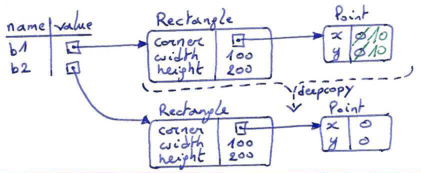
Now b1 and b2 are completely separate objects.

Glossary

deep copy

To copy the contents of an object as well as any embedded objects, and any objects embedded in them, and so on; implemented by the deepcopy function in the copy module.

deep equality

Equality of values, or two references that point to (potentially different) objects that have the same attribute values.

shallow copy

To copy the contents of an object, including any references to embedded objects; implemented by the copy function in the copy module.

shallow equality

Equality of references, or two references that point to the same object.

string converter method

A magic method in Python (called __str__) that produces an informal string representation of an object. For example, this is the string that will be printed when calling the print function on that object.

References