Embedded references

We have seen examples of attributes that refer to other objects. For example, the CardGame class referred to a Deck object as one of its attributes. We call such objects contained in another one embedded references.

We have also seen examples of data structures, such as lists and tuples. For example, Deck objects contain a list of Card objects.

A data structure is a mechanism for grouping and organising data to make it easier to use.

In this section, we will use object-oriented programming and objects with embedded references to define our own data structure, a data structure commonly known as a linked list.

Linked lists are made up of Node objects, where each node (the last node excepted) contains a reference to the next node in the linked list. In addition, each node carries a unit of data called its cargo.

A linked list can be regarded as a recursive data structure because it has a recursive definition:

A linked list is either:

1. the empty list, represented by None, or
2. a node that contains a cargo object and a reference to a linked list.

Recursive data structures lend themselves to recursive methods. A recursive method is a method that invokes itself, typically on a subset of the data on which it was originally invoked. For example, a method to print a linked list could first print the cargo of the node at the head of the list, and then recursively invoke itself on the embedded linked list that node refers to.

The Node class

As always when writing a new class, we'll start with the initialisation and __str__ methods so that we can test the basic mechanism of creating and displaying the new type:

class Node:
    """ Represents a Node in a LinkedList data structure. """

    def __init__(self, cargo=None, next=None):
        """
        Creates a new Node object.
        @pre:  -
        @post: A new Node object has been initialised.
           A node can contain a cargo and a reference to another node.
           If none of these are given, the node is initialised with
           empty cargo (None) and no reference (None).
        """
        self.cargo = cargo
        self.next  = next

    def __str__(self):
        """
        @pre:  -
        @post: Returns a print representation of the cargo
               contained in this Node.
        """
        return str(self.cargo)

As usual, the parameters for the initialisation method are optional. By default, both the cargo and the link to the next node, are set to None.

The string representation of a node is just the string representation of its cargo. Since any value can be passed to the str function, we can store any value in a linked list.

To test the implementation so far, we can create a Node object and print it:

>>> node = Node("test")
>>> print(node)
test

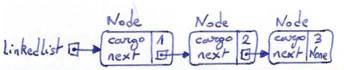
To make it more interesting, we will now try to create a linked list with three nodes. First we create each of the three nodes.

>>> node1 = Node(1)
>>> node2 = Node(2)
>>> node3 = Node(3)

This code creates three nodes, but we don't have a linked list yet because the nodes are not linked. The memory diagram looks like this:

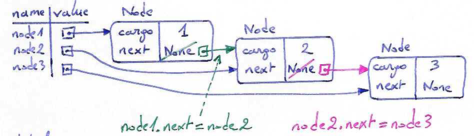
To link the nodes, we have to make the first node refer to the second one and the second one to the third:

>>> node1.next = node2
>>> node2.next = node3
>>> linkedlist = node1

The next reference of the third node remains None, which indicates that it is the end of the linked list. Now the memory diagram looks like this:

Now you know how to create nodes and link them into lists. What might be less clear at this point is why.

Linked lists as collections

Linked lists and other data structures are useful because they provide a way to assemble multiple objects into a single entity, sometimes called a collection. In our example, the first node of a linked list serves as a reference to the entire list (since from the first node, all the other nodes in the list can be reached).

To pass a linked list as a parameter, we only have to pass a reference to its first node. For example, the function print_list below takes a single node as an argument. Starting with the head of a linked list, it prints each node until it gets to the end:

def print_list(node):
    """
    Prints the cargo of this node and of each node it is linked to.
    @pre:  node is an instance of class Node
    @post: Has printed a space-separated list of the form "a b c ... ",
           where "a" is the string-representation of this node,
           "b" is the string-representation of my next node, and so on.
           A space is printed after each printed value.
    """
    while node is not None:
        print(node, end=" ")
        node = node.next

To invoke this function, we pass a reference to the first node:

>>> print_list(node1)
1 2 3

Inside print_list we have a reference to the first node of the linked list. From there, to get to the next nodes, we can use the next attribute of each node. To traverse a linked list, it is common to use a loop variable like node to refer to each of the nodes in succession. This diagram shows the different values that the node variable takes on:

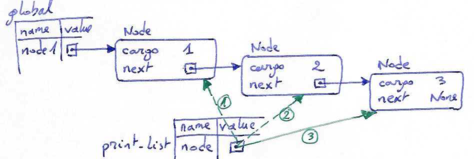
Linked lists and recursion

Since the linked list data structure is defined as a class, it would have been more natural to define the print_list function as a method on the Node class. When doing so, the method needs to be defined in a recursive way, by first printing the cargo of its head and then recursively invoking the print_list method on the next node, until no more nodes are left:

class Node:
    ...

    def print_list(self):
        """
        Prints the cargo of this node and then recursively
        of each node connected to this one.
        @pre:  The linked data structure of which this node is the head
               contains no loops.
        @post: Has printed a space-separated list of the form "a b c ... ",
               where "a" is the string-representation of this node,
               "b" is the string-representation of my next node, and so on.
               A space is printed after each printed value.
        """
        print(self, end=" ")  # print my head
        tail = self.next      # go to my next node
        if tail is not None : # as long as the end of the list was not reached
            tail.print_list() # recursively print remainder of the list

To call this method, we just send it to the first node:

>>> node1.print_list()
1 2 3

In general, it is natural to express many operations on linked lists as recursive methods. The following is a recursive algorithm for printing a list backwards:

1. Separate the list into two pieces: its first node (called the head); and the remainder (called the tail).
2. Print the tail backward.
3. Print the head.

The code which implements this algorithm looks surprisingly similar to the code of the print_list method above, the only difference being that now the head is printed after the recursive call, instead of before :

class Node:
    ...

    def print_backward(self):
        """
        Recursively prints the cargo of each node connected to this node (in
        opposite order), then prints the cargo of this node as last value.
        @pre:  The linked data structure of which this node is the head
               contains no loops.
        @post: Has printed a space-separated list of the form "... c b a",
               where a is my cargo (self), b is the cargo of the next node,
               and so on. The nodes are printed in opposite order: the
               last node's value is printed first.
        """
        tail = self.next           # go to my next node
        if tail is not None :      # as long as end of list was reached
            tail.print_backward()  # recursively print remainder backwards
        print(self, end = " ")     # print my head

As before, to call this method, we just send it to the first node:

>>> node1.print_backward()
3 2 1

Can we prove that print_backward will always terminate? In fact, the answer is no: some (ill-formed) linked lists can make this method crash.

Infinite lists

There is nothing to prevent a node from referring back to an earlier node in the list, including itself. For example, this figure shows a list with two nodes, one of which refers to itself:

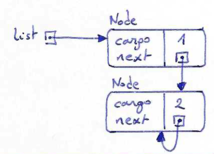
We could create such an infinite list as follows:

>>> node1 = Node(1)
>>> node2 = Node(2)
>>> node1.next = node2
>>> node2.next = node2

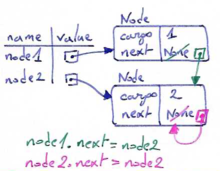
If we call either print_list or print_backward on this list, it will try to recurse infinitely, which soon leads to an error like:

RecursionError: maximum recursion depth exceeded

This sort of behaviour makes infinite lists difficult to work with. Nevertheless, they are occasionally useful. For example, we might represent a number as a list of digits and use an infinite list to represent a repeating fraction.

Regardless, it is problematic that we cannot prove that print_list and print_backward terminate. The best we can do is the hypothetical statement, "if the list contains no loops, then these methods will terminate", and use this as a precondition to be satisfied by the methods.

Ambiguity between lists and nodes

When looking at the code of the print_list or print_backward methods above, there is sometimes ambiguity between whether a reference to a node should be interpreted as a reference to a single node or rather as a reference to an entire linked list having that node as its first node.

For example, when we write print(self, end=" ") we seem to regard self as referring to a single node that is the head of this linked list, and we use the print function to print the value of its cargo.

On the other hand, when assigning self.next to a variable named tail, we seem to be regarding self.next not as a single node but rather as the entire linked list that has the next node as first node.

The fundamental ambiguity theorem describes the ambiguity that is inherent in a reference to a node of a linked list: A variable that refers to a node of a linked list might treat the node as a single object or as the first in a list of nodes.

Modifying lists

There are two ways to modify a linked list. Obviously, we can change the cargo of one of its nodes, but the more interesting operations are the ones that add, remove, or reorder nodes.

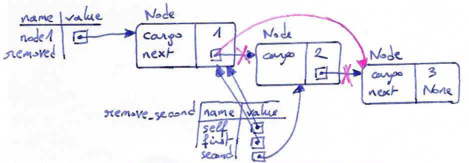
As an example, let's write a method that removes the second node in the list and returns a reference to the removed node:

class Node:
    ...

    def remove_second(self):
        """
        @pre:  The linked data structure of which this node
               is the first node contains no loops.
        @post: Does nothing if the linked list with this node
               as head has no second node;
               else removes the second node from this linked
               list, and returns a reference to the removed
               and unlinked second node.
        """
        first = self
        second = self.next
        # do nothing if there is no second node
        if second is None: return
        # Make the first node refer to the third
        first.next = second.next
        # Separate the second node from the rest of the list
        second.next = None
        return second

We are using temporary variables first and second here to make the code more readable. Here is how to use this method:

>>> node1.print_list()
1 2 3
>>> removed = node1.remove_second()
>>> removed.print_list()
2
>>> node1.print_list()
1 3

This state diagram shows the effect of the operation:

Wrappers and helpers

It is often useful to divide a list operation into two methods. For example, to print a list backward in a more conventional format [3 2 1], we can use the print_backward method to print 3 2 1 but we need a separate method to print the brackets. Let's call it print_backward_nicely:

class Node:
    ...
    def print_backward_nicely(self):
        """
        @pre:  The linked data structure of which this node is the head
               contains no loops.
        @post: Has printed a space-separated list of the form "[ ... c b a ]",
               where a is my cargo (self), b is the cargo of the next node,
               and so on. The nodes are printed in opposite order: the
               last node's value is printed first. A space is printed after
               and before the opening and closing bracket, as well as between
               any two elements. An empty linked is printed as "[ ]"
        """
        print("[", end=" ")
        self.print_backward()
        print("]")

When we use this method elsewhere in the program, we invoke print_backward_nicely directly, and it invokes print_backward on our behalf. In that sense, print_backward_nicely acts as a wrapper, and it uses print_backward as a helper.

The LinkedList class

There remains a subtle problem with the way we have been implementing linked lists so far, namely that the empty list is represented in a different way (None) as a non-empty list (a collection of Node objects chained to each other). To solve this problem, we will create a new class called LinkedList. Its attributes are an integer that contains the length of the list and a reference to the first node. In case of an empty list the length attribute is 0 and the reference to the first node is None. LinkedList objects serve as handles for manipulating lists of Node objects:

class LinkedList:
    """ Represents a linked list datastructure. """

    def __init__(self):
        """
        Initialises a new LinkedList object.
        @pre:  -
        @post: A new empty LinkedList object has been initialised.
               It has 0 length, contains no nodes and its head points to None.
        """
        self.length = 0
        self.head = None

Adding an element to the front of a LinkedList object can be defined straightforwardly. The method add is a method for LinkedLists that takes an item of cargo as an argument and puts it in a newly created note at the head of the list. This works regardless of whether the list is initially empty or not.

class LinkedList:
    ...

    def add(self, cargo):
        """
        Adds a new Node with given cargo to the front of this LinkedList.
        @pre:  self is a (possibly empty) LinkedList.
        @post: A new Node object is created with the given cargo.
               This new Node is added to the front of the LinkedList.
               The length counter has been incremented.
               The head of the list now points to this new node.
               Nothing is returned.
        """
        node = Node(cargo)
        node.next = self.head
        self.head = node
        self.length += 1

The LinkedList class also provides a natural place to put wrapper functions like our method print_backward_nicely, which we can make a method of the LinkedList class:

class LinkedList:
    ...

    def print_backward(self):
        """
        Prints the contents of this LinkedList and its nodes, back to front.
        @pre:  self is a (possibly empty) LinkedList
        @post: Has printed a space-separated list of the form "[ ... c b a ]",
               where "a", "b", "c", ... are the string representation of each
               of the LinkedList's nodes. The nodes are printed in opposite order:
               the last nodes' value are printed first.
               A space is printed after and before the opening and closing bracket,
               as well as between any two elements.
               An empty linked is printed as "[ ]"
        """
        print("[", end=" ")
        if self.head is not None:
            self.head.print_backward()
        print("]")

We renamed print_backward_nicely to print_backward when defining it on the LinkedList class. This is a nice example of polymorphism. There are now two methods named print_backward: the original one defined on the Node class (the helper); and the new one on the LinkedList class (the wrapper). When the wrapper method invokes self.head.print_backward(), it is invoking the helper method, because self.head is a Node object. To avoid calling this helper method on an empty list (when self.head is None), we added a condition to check for that situation.

In a similar way we can define a print method on the LinkedList class, to print the entire list nicely with surrounding brackets. This method is implemented in a very similar way to the print_backward method, using the print_list method on the Node class as a helper method.

class LinkedList:
    ...

    def print(self):
        """
        Prints the contents of this LinkedList and its nodes.
        @pre:  self is a (possibly empty) LinkedList
        @post: Has printed a space-separated list of the form "[ a b c ... ]",
               where "a", "b", "c", ... are the string representation of each
               of the linked list's nodes.
               A space is printed after and before the opening and closing bracket,
               as well as between any two elements.
               An empty linked is printed as "[ ]"
        """
        print("[", end=" ")
        if self.head is not None:
            self.head.print_list()
        print("]")

The code below illustrates how to create and print linked lists using this new LinkedList class.

>>> l = LinkedList()
>>> print(l.length)
0
>>> l.print()
[ ]
>>> l.add(3)
>>> l.add(2)
>>> l.add(1)
>>> l.print()
[ 1 2 3 ]
>>> l.print_backward()
[ 3 2 1 ]

The full code of this LinkedList class and its corresponding Node class are provided in an appendix. As opposed to the code above, in this appendix we also hid the attributes and provided some accessor and mutator methods to access and modify these attributes.

Other useful methods can be added to this LinkedList class, such as a method to remove the first element of a list. We leave this as an exercise to the reader.

Invariants

Some lists are well formed; others are not. For example, if a list contains a loop, it will cause many of our methods to crash, so we might want to require that lists contain no loops. Another requirement is that the length value in the LinkedList object should be equal to the actual number of nodes in the list.

Requirements like these are called invariants because, ideally, they should be true of every object all the time. Specifying invariants for objects is a useful programming practice because it makes it easier to prove the correctness of code, check the integrity of data structures, and detect errors.

One thing that is sometimes confusing about invariants is that there are times when they are violated. For example, in the middle of add, after we have added the node but before we have incremented length, the invariant is violated. This kind of violation is acceptable; in fact, it is often impossible to modify an object without violating an invariant for at least a little while. Normally, we require that every method that violates an invariant must restore the invariant.

If there is any significant stretch of code in which the invariant is violated, it is important for the comments to make that clear, so that no operations are performed that depend on the invariant.

Glossary

cargo

An item of data contained in a node. (The data carried by the node.)

collection

A collection is a data structure that assembles multiple objects into a single entity.

data structure

A mechanism for grouping and organising data to make it easier to use.

embedded reference

A reference to another object stored in an attribute of an object.

fundamental ambiguity theorem

A reference to a list node can be treated as a single object or as the first in a list of nodes.

helper

A method that is not invoked directly by a caller but is used by another method to perform part of an operation. Also called auxiliary method.

invariant

An assertion that should be true of an object at all times (except perhaps while the object is being modified).

link

An embedded reference used to link one object to another.

linked list

A data structure that implements a collection of elements using a sequence of linked nodes.

node

An element of a linked list, usually implemented as an object that carries a unit of data (its cargo) and that contains an embedded reference (a link) to another object of the same type.

precondition

An assertion that must be true in order for a method to work correctly.

recursive data structure

A recursive data structure, such as a linked list, is a data structure that can be defined in terms of itself. For example, we can say that a linked list is either the empty list, or a node that carries a cargo and a link to a linked list, containing the remaining data.

recursive method

A recursive method is a method that invokes itself, typically on a subset of the data on which it was originally invoked.

singleton

A linked list with a single node.

wrapper

A method that acts as a middleman between a caller and a helper method, often making the method easier or less error-prone to invoke.

References