MyTime

As another example of a user-defined class, we'll define a class called MyTime that records the time of day. We provide an __init__ method to ensure that every instance is created with appropriate attributes and initialisation. The class definition looks like this:

class MyTime:

    def __init__(self, hrs=0, mins=0, secs=0):
        """
        @pre:  hrs, mins, secs are positive integers;
               0 <= mins < 60, 0 <= secs < 60;
               if not supplied a default value of 0 is used
        @post: the attributes hours, minutes and seconds of this
               MyTime object have been initialised to hrs, mins, secs
               (or 0 if no values were supplied)
        """
        self.hours = hrs
        self.minutes = mins
        self.seconds = secs

We can then create and instantiate a new MyTime object by calling the constructor with the necessary arguments for the initialisation method:

tim1 = MyTime(11, 59, 30)

The memory diagram for this object looks like this:

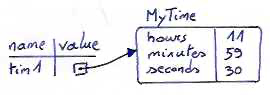
We leave it as an exercise for the reader (please do it!) to also add a __str__ method so that MyTime objects can print themselves decently. For example, the object above should print as 11:59:30. (If you don't know how to do this, look at the Rectangle class of the previous chapter for inspiration.)

Pure functions

In the next few sections, we'll write two versions of a function called add_time, which calculates the sum of two MyTime objects. They will demonstrate two kinds of functions: pure functions and modifiers.

The following is a first rough version of add_time:

def add_time(t1, t2):
    """
    @pre:  t1 and t2 are instances of class MyTime
    @post: a new MyTime object is returned of which the
           hours, minutes and seconds attributes are the
           sum of the respective attributes in t1 and t2
    """
    h = t1.hours + t2.hours
    m = t1.minutes + t2.minutes
    s = t1.seconds + t2.seconds
    sum_t = MyTime(h, m, s)
    return sum_t

The function creates a new MyTime object and returns a reference to the new object. This is called a pure function because it does not modify any of the objects passed to it as parameters and it has no side effects, such as updating global variables, displaying a value, or getting user input.

Here is an example of how to use this function. We'll create two MyTime objects: current_time, which contains the current time; and bread_time, which contains the amount of time it takes for a breadmaker to make bread. Then we'll use add_time to figure out when the bread will be done.

>>> current_time = MyTime(9, 14, 30)
>>> bread_time = MyTime(3, 35, 0)
>>> done_time = add_time(current_time, bread_time)
>>> print(done_time)
12:49:30

The output of this program is 12:49:30, which is correct. On the other hand, there are cases where the result is not correct. Can you think of one?

The problem is that this function does not deal with cases where the number of seconds or minutes adds up to more than sixty. When that happens, we have to carry the extra seconds into the minutes column or the extra minutes into the hours column.

Here's an improved version of the function. (We left out its specification, because it would get pretty big and we will soon propose a better alternative solution.)

def add_time(t1, t2):

    h = t1.hours + t2.hours
    m = t1.minutes + t2.minutes
    s = t1.seconds + t2.seconds

    if s >= 60:
        s -= 60
        m += 1

    if m >= 60:
        m -= 60
        h += 1

    sum_t = MyTime(h, m, s)
    return sum_t

This function is already starting to get bigger, and still doesn't work for all possible cases. Later we will suggest an alternative approach that yields better code.

Modifiers

There are times when it is useful for a function to modify one or more of the objects it gets as parameters. Usually, the caller keeps a reference to the objects it passes, so any changes the function makes are visible to the caller. Functions that work this way are called modifiers.

For example, increment, which adds a given number of seconds to a MyTime object, when written as a modifier, could behave like this:

>>> t = MyTime(10,20,30)
>>> increment(t,70)
>>> print(t)
10:21:40

A rough draft of the implementation of this function looks like this:

def increment(t, secs):
    """
    @pre:  t is an instance of MyTime;
           secs is a positive integer
    @post: the seconds attribute of t is modified by adding secs;
           if the amount of seconds in t becomes > 60,
           each surplus of 60 seconds spills over to an extra
           minute added to the minutes attribute of t;
           if the amount of minutes in t becomes > 60,
           each surplus of 60 minutes spills over to an extra
           hour added to the hours attribute of t;
           nothing is returned
    """
    t.seconds += secs

    if t.seconds >= 60:
        t.seconds -= 60
        t.minutes += 1

    if t.minutes >= 60:
        t.minutes -= 60
        t.hours += 1

The first line performs the basic operation; the remainder deals with the special cases we saw before.

Note that this function has no return statement nor does it need to create a new object. It simply modifies the state of the Time object t that was passed as first parameter to the function.

Is this function correct? What happens if the parameter secs is much greater than sixty? In that case, it is not enough to carry once; we have to keep doing it until t.seconds is less than sixty. One solution is to replace the if statements with while statements:

def increment(t, secs):

    # SAME SPECIFICATION AS BEFORE

    t.seconds += secs

    while t.seconds >= 60:
        t.seconds -= 60
        t.minutes += 1

    while t.minutes >= 60:
        t.minutes -= 60
        t.hours += 1

This function is now correct when seconds is not negative, but it is still not a particularly good nor efficient solution.

>>> t = MyTime(10,20,30)
>>> increment(t,100)
>>> print(t)
10:22:10

Converting increment to a method

Once again, since object-oriented programmers would prefer to put functions that work with MyTime objects directly into the MyTime class, let's convert increment to a method. To save space, we will leave out previously defined methods in that class, but you should keep them in your version:

class MyTime:

    # Previous method definitions here...

    def increment(self, seconds):

        # SAME SPECIFICATION AS BEFORE

        self.seconds += seconds

        while self.seconds >= 60:
            self.seconds -= 60
            self.minutes += 1

        while self.minutes >= 60:
            self.minutes -= 60
            self.hours += 1

The transformation is purely mechanical: we move the definition into the class definition and change the name of the first parameter (and all occurrences of that parameter in the method body) to self, to fit with Python style conventions.

Now we can invoke increment using the dot syntax for invoking a method, instead of writing increment(current_time,500) :

>>> current_time = MyTime(11, 58, 30)
>>> current_time.increment(500)
>>> print(current_time)
12: 6:50

The object current_time on which the method is invoked gets assigned to the first parameter, self. The second parameter, seconds gets the value 500.

An "Aha!" moment

An "Aha!" moment is that moment or instant at which the solution to a problem suddenly becomes clear. Often a high-level insight into a problem can make the programming much easier.

A three-digit number in base 10, for example the number 284, can be represented by 3 digits, the right most one (4) representing the units, the middle one (8) representing the tens, and the left-most one representing the hundreds. In other words, 284 = 2*100 + 8*10 + 4*1.

Our "Aha!" moment consists of the insight that a MyTime object is actually a three-digit number in base 60 ! The "seconds" correspond to the units, the "minutes" to the sixties, and the hours to the thirty-six hundreds. Indeed, 12h03m30s corresponds to 12*3600 + 3*60 + 30 = 43410 seconds.

When we were writing the add_time and increment functions and methods, we were effectively doing addition in base 60, which explains why we had to carry over remaining digits from one column to the next.

This observation suggests another approach to the entire problem --- we can convert a MyTime object into a single number (in base 10, representing the seconds) and take advantage of the fact that the computer knows how to do arithmetic with numbers. The following method can be added to the MyTime class to convert any instance into a corresponding number of seconds:

class MyTime:
    # ...

    def to_seconds(self):
        """
        @pre:  -
        @post: returns the total number of seconds represented
               by this instance of MyTime
        """
        return self.hours * 3600 + self.minutes * 60 + self.seconds

>>> current_time = MyTime(11, 58, 30)
>>> seconds = current_time.to_seconds()
>>> print(current_time)
11:58:30
>> print(seconds)
43110

Now, all we need is a way to convert from an integer, representing the time in seconds, back to a MyTime object. Supposing we have tsecs seconds, some integer division and modulus operators can do this for us:

hrs = tsecs // 3600
leftoversecs = tsecs % 3600
mins = leftoversecs // 60
secs = leftoversecs % 60

You might have to think a bit to convince yourself that this technique to convert from one base to another is correct. Remember that the // operator represents integer division and that the modulus operator % calculates the remainder of integer division.

As mentioned in the previous sections, one of the main goals of object-oriented programming is to wrap together data with the operations that apply to it. So we'd like to put the above conversion logic inside the MyTime class. A good solution is to rewrite the class initialisation method __init__ so that it can cope with initial values of seconds or minutes that are outside the normalised values. (A normalised time would be something like 3 hours 12 minutes and 20 seconds. The same time, but unnormalised could be 2 hours 70 minutes and 140 seconds, where the minutes or seconds are more than the expected maximum of 60.)

Let's rewrite a more powerful initialiser for MyTime:

class MyTime:
   # ...

   def __init__(self, hrs=0, mins=0, secs=0):
       """ Create a new MyTime object initialised to hrs, mins, secs.
           @pre:  hrs, mins, secs are positive integers;
                  if not supplied a default value of 0 is used
           @post: the attributes hours, minutes and seconds of this
                  MyTime object have been initialised to hrs, mins, secs
                  (or 0 if no values were supplied)
                  In case the values of mins and secs are outside the range
                  0-59, the resulting MyTime object will be normalised,
                  so that they are in this range
       """

       # Calculate the total number of seconds to represent
       totalsecs = hrs*3600 + mins*60 + secs
       self.hours = totalsecs // 3600        # Split in h, m, s
       leftoversecs = totalsecs % 3600
       self.minutes = leftoversecs // 60
       self.seconds = leftoversecs % 60

Now we can rewrite add_time like this:

def add_time(t1, t2):
    """
    @pre:  t1 and t2 are instances of class MyTime
    @post: a new MyTime object is returned of which the
           total time in seconds is the sum of the total
           time in seconds of t1 and t2
    """
    secs = t1.to_seconds() + t2.to_seconds()
    return MyTime(0, 0, secs)

This version is much shorter than the original, and it is much easier to demonstrate or reason that it is correct. Notice that we didn't have to do anything for carrying over seconds or minutes that are too large; that is handled automatically by our new initialiser method now. (Isn't that just wonderful?)

>>> current_time = MyTime(9, 14, 30)
>>> bread_time = MyTime(3, 35, 0)
>>> done_time = add_time(current_time, bread_time)
>>> print(done_time)
12:49:30

Note that we could also implement add_time as a method defined on the class MyTime rather than as a globally defined function, but we will leave that to the next chapter.

The final question that remains now is how we can rewrite the increment method that we wrote before, without having to reimplement the logic that we now put into our new initialiser method. The answer to this question is in the question. What if we simply try to call the __init__ method from within the increment method so as to reuse its logic. This can be done surprisingly easily:

def increment(self, secs):
    """
    @pre:  t is an instance of MyTime;
           secs is a positive integer
    @post: the seconds attribute of t is modified by adding secs;
           if necessary t gets normalized so that neither the
           amount of seconds in t nor the amount of minutes in t
           becomes > 60;
           nothing is returned
    """
    self.__init__(self.hours,self.minutes,self.seconds+secs)

Again, the carrying over of seconds or minutes that are too large is handled automatically by the initialiser method. It is important to observe that, as opposed to the add_time method, we are not creating a new MyTime object here. We are simply calling __init__ to assign a new state to the existing instance (self).

>>> current_time = MyTime(11, 58, 30)
>>> current_time.increment(500)
>>> print(current_time)
12: 6:50

Generalisation

In some ways, converting from base 60 to base 10 and back is harder than just dealing with time. Base conversion is more abstract; our intuition for dealing with time is better.

However, if we have the insight to treat time objects as base 60 numbers and make the investment of writing the conversions, we get a program that is shorter, easier to read and debug, and more reliable.

It is also easier to add features later. For example, imagine subtracting two MyTime objects to find the duration between them. The naive approach would be to implement subtraction with borrowing. Using the conversion functions would be easier and more likely to be correct.

Ironically, sometimes making a problem harder (or more general) makes the programming easier, because there are fewer special cases and fewer opportunities for error.

Glossary

functional programming style

A style of program design in which the majority of functions are pure.

generalisation

A problem-solving technique where a concrete problem gets generalised into a more abstract one that is easier to solve

modifier

A function or method that changes one or more of the objects it receives as parameters. Most modifier functions are void (do not return a value).

normalized

Data is said to be normalized if it fits into some reduced range or set of rules. We usually normalize our angles to values in the range [0..360[. We normalize minutes and seconds to be values in the range [0..60[. And we'd be surprised if the local store advertised its cold drinks at "One dollar, two hundred and fifty cents".

pure function

A function that does not modify any of the objects it receives as parameters. Most pure functions are not void but return a value.

specialisation

A problem-solving technique where a more abstract problem gets specialised into a more concrete one that is easier to solve

References