Composition

By now, we have seen several examples of composition. One example is using a method invocation as part of an expression. Another example is the nested structure of statements: we can put an if statement within a while loop, within another if statement, and so on.

Having seen this pattern, and having learned about lists and objects, we should not be surprised to learn that we can create lists of objects. We can also create objects that contain lists (as attributes); we can create lists that contain lists; we can create objects that contain objects; and so on.

In this chapter and the next, we will look at some examples of these combinations, using Card objects as an example.

Card objects

If you are not familiar with common playing cards, now would be a good time to get a deck, or else this chapter might not make much sense. There are fifty-two cards in a deck, each of which belongs to one of four suits and one of thirteen ranks. The suits are Spades ♠︎, Hearts ♥︎, Diamonds ♦︎, and Clubs ♣︎ (in descending order in the bridge game). The ranks are Ace (1), 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, and King. Depending on the game that we are playing, the rank of Ace may be higher than King or lower than 2. The rank is sometimes called the face-value of the card.

If we want to define a new object to represent a playing card, it is obvious what its attributes should be: rank and suit. It is not as obvious what type these attributes should have. One possibility is to use strings containing words like "Spade" for suits and "Queen" for ranks. One problem with this implementation is that it would not be easy to compare cards to see which had a higher rank or suit.

An alternative is to use integers to encode the ranks and suits. By encode, we do not mean what some people think, which is to encrypt or translate into a secret code. What a computer scientist means by encode is to define a mapping between a sequence of numbers and the items he or she wants to represent. For example:

Spades   <-->  3
Hearts   <-->  2
Diamonds <-->  1
Clubs    <-->  0

An obvious feature of this mapping is that the suits map to integers in order, so we can compare suits by comparing integers. The mapping for ranks is fairly obvious; each of the numerical ranks maps to the corresponding integer (and Ace to 1), and for face cards:

Jack   <-->  11
Queen  <-->  12
King   <-->  13

Using such an encoding of suits and ranks as integers, the class definition for the Card type looks like this:

class Card:
    """ Represents a Card in a Deck of playing cards. """

    def __init__(self, suit=0, rank=0):
        self.suit = suit
        self.rank = rank

As usual, we provide an initialisation method that takes an optional parameter for each attribute. (We'll explain later why we chose 0 as default value for the rank, even though 0 does not map to any existing rank.)

To create some objects, representing say the 3 of Clubs (0) and the Jack (11) of Diamonds (1), use these commands:

three_of_clubs = Card(0, 3)
card1 = Card(1, 11) # Jack of Diamonds

In the first case above, the first argument, 0, represents the suit Clubs. In the second case above, the second argument, 11, represents the Jack.

Class attributes

In order to print Card objects in a way that people can easily read, we want to map the integer codes back onto words. A natural way to do that is with lists of strings. We assign these lists to class attributes (or class variables) at the top of the class definition:

class Card:
    """ Represents a Card in a Deck of playing cards. """

    suits = ["Clubs", "Diamonds", "Hearts", "Spades"]
    ranks = ["narf", "Ace", "2", "3", "4", "5", "6", "7",
             "8", "9", "10", "Jack", "Queen", "King"]

    def __init__(self, suit=0, rank=0):
        self.suit = suit
        self.rank = rank

    def __str__(self):
        return (Card.ranks[self.rank] + " of " + Card.suits[self.suit])

A class attribute or class variable is defined outside of any method, and it can be accessed from any of the methods in the class. To access a class attribute, you have to use the dot notation. Card.ranks refers to the class attribute ranks defined in the class Card.

Inside __str__, we can use the suits and ranks list to map the numerical values of suit and rank to strings. For example, the expression Card.suits[self.suit] means: use the instance variable suit from the object self as an index into the class attribute named suits of the class Card, and select the corresponding string.

The reason for the "narf" value (which is an acronym for "not a real face-value") as the first element in ranks is to act as a place keeper for the zero-eth element of the list, which will never be used. The only valid ranks are 1 to 13. This wasted item is not entirely necessary. We could have started at 0, by putting rank 1 at position 0 in the list, and so on, but it is much less confusing to encode the rank 2 as integer 2, 3 as 3, and so on.

With the methods we have so far, we can create and print cards:

>>> card1 = Card(1, 11)
>>> print(card1)
Jack of Diamonds

We can access a class variable directly via its class, like we did before:

>>> print(Card.suits[1])
Diamonds

Again, it can be useful to draw a memory diagram like the one below to clearly understand that instance variables are stored in the instance and that class variables are part of the class definition:

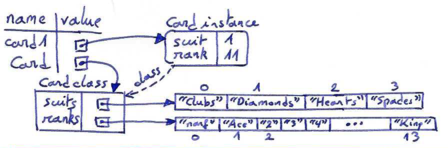
Alternatively, we can access a class variable via the object, for example:

>>> print(card1.suits[1])
Diamonds

What actually happens when accessing the variable suits on the object card1, is that Python will first try to find an instance variable with that name, and if that doesn't exist, following the link to the class of this instance look for a class variable with that name. This means that we could also have implemented the __str__ method above as follows (it will first look for a variable on the object itself, and if it doesn't find it there look in the class):

def __str__(self):
    return (self.ranks[self.rank] + " of " + self.suits[self.suit])

Personally, I prefer the former notation where it is also more explicit that we are actually accessing a class variable.

Unlike instance variables, which can have different values for each different instance of a same class, class attributes are shared by all instances of the same class. The advantage of this is that we can use any Card object to access the class attributes:

>>> card2 = Card(1, 3)
>>> print(card2)
3 of Diamonds
>>> print(card2.suits[1])
Diamonds

However, because every Card instance references the same class attribute, we have an aliasing situation. The disadvantage of that is that if we would modify a class attribute, this modification would affect every instance of that class. For example, if we decide that Jack of Diamonds should really be called Jack of Swirly Whales, we could do this:

>>> card1.suits[1] = "Swirly Whales"
>>> print(card1)
Jack of Swirly Whales

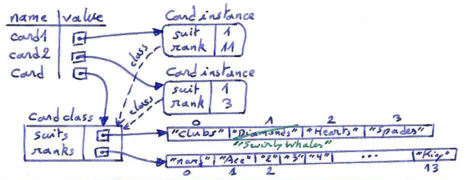
The problem is that all of the Diamonds just became Swirly Whales:

>>> print(card2)
3 of Swirly Whales

It is usually not a good idea to modify class attributes. If you do, be aware that the value will change for all instances of that class.

Comparing cards

For primitive types, there are six relational operators ( <, >, ==, <=, >=, !=) that compare values and determine when one is greater than, less than, or equal to another. If we want our own types to be comparable using the syntax of these relational operators, we need to define six corresponding magic methods in our class.

We'd like to start with a single method named cmp that captures the logic of ordering. By convention, a comparison method takes two parameters, self and other, and returns 1 if the first object is greater, -1 if the second object is greater, and 0 if they are equal to each other.

Some types are completely ordered, which means that we can compare any two elements and tell which is bigger. For example, the integers and the floating-point numbers are completely ordered. Some types are unordered, which means that there is no meaningful way to say that one element is bigger than another. For example, the fruits are unordered, which is why we cannot compare apples and oranges, and we cannot meaningfully order a collection of images, or a collection of cellphones.

Playing cards are partially ordered, which means that sometimes we can compare cards and sometimes not. For example, we know that the 3 of Clubs is higher than the 2 of Clubs, and the 3 of Diamonds is higher than the 3 of Clubs. But which is better, the 3 of Clubs or the 2 of Diamonds? One has a higher rank, but the other has a higher suit.

In order to make cards comparable, we have to decide which is more important, rank or suit. To be honest, the choice is arbitrary. For the sake of choosing, we will say that suit is more important, because a new deck of cards comes sorted with all the Clubs together, followed by all the Diamonds, and so on.

With that decided, we can write cmp:

def cmp(self, other):
    # Check the suits
    if self.suit > other.suit: return 1
    if self.suit < other.suit: return -1
    # Suits are the same... check ranks
    if self.rank > other.rank: return 1
    if self.rank < other.rank: return -1
    # Ranks are the same... it's a tie
    return 0

Note that in this ordering, Aces (1) appear lower than Deuces (2).

Now, we can define the six magic methods that do the overloading of each of the relational operators for us:

def __eq__(self, other):
    # equality
    return self.cmp(other) == 0

def __le__(self, other):
    # less than or equal
    return self.cmp(other) <= 0

def __ge__(self, other):
    # greater than or equal
    return self.cmp(other) >= 0

def __gt__(self, other):
    # strictly greater than
    return self.cmp(other) > 0

def __lt__(self, other):
    # strictly less than
    return self.cmp(other) < 0

def __ne__(self, other):
    # not equal
    return self.cmp(other) != 0

With this machinery in place, the relational operators now work as we'd like them to:

>>> card1 = Card(1, 11)
>>> card2 = Card(1, 3)
>>> card3 = Card(1, 11)
>>> card1 < card2
False
>>> card1 == card3
True

Decks

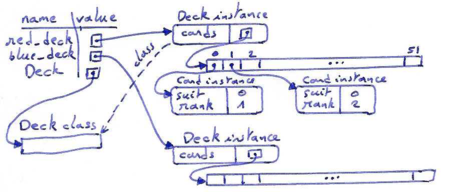
Now that we have objects to represent Cards, the next logical step is to define a class to represent a Deck. Of course, a deck is made up of cards, so each Deck object will contain a list of cards as an attribute. Some card games will need at least two different decks --- a red deck and a blue deck.

The following is a class definition for the Deck class. The initialisation method creates the attribute cards and generates the standard pack of fifty-two cards:

class Deck:
    def __init__(self):
        self.cards = []
        for suit in range(4):
            for rank in range(1, 14):
                self.cards.append(Card(suit, rank))

The easiest way to populate the deck is with a nested loop. The outer loop enumerates the suits from 0 to 3. The inner loop enumerates the ranks from 1 to 13. (Remember that range(m, n) generates integers from m up to, but not including, n.) Since the outer loop iterates four times, and the inner loop iterates thirteen times, the total number of times the body is executed is 52 (13 * 4). Each iteration creates a new instance of Card with the current suit and rank, and appends that card to the cards list. (Remember that whenever the Card constructor method is invoked a new instance of class Card is created.)

With this in place, we can instantiate some decks:

red_deck = Deck()
blue_deck = Deck()

Printing the deck

As usual, when we define a new type we would like a way to print the contents of a Deck instance. One way to do so would be to implement a method to traverse the list of cards in the deck and print each Card:

class Deck:
    ...
    def print_deck(self):
        for card in self.cards:
            print(card)

Here, and from now on, the ellipsis (...) indicates that we have omitted the other methods in the class.

>>> red_deck.print_deck()

However, as we don't like chatterbox methods that call print, a better alternative to print_deck would be to write a string conversion method __str__ for the Deck class. The advantage of __str__ is that it is more flexible. Rather than just printing the contents of the object, it generates a string representation that other parts of the program can manipulate before printing, or store for later use. Here is a version of __str__ that returns a string representation of a Deck. To add a bit of flair to it, it arranges the cards in a cascade where each card is indented one space more than the previous card:

class Deck:
    ...
    def __str__(self):
        s,spaces = "",""
        for c in self.cards:
            s = s + spaces + str(c) + "\n"
            spaces += " "
        return s

This example demonstrates several features. First, instead of looping over the range of all cards, using an expression like for i in range(len(self.cards)), and to access each card using its index i, as in self.cards[i], instead we simply traverse self.cards and assign each card to a variable c.

Second, instead of using the print command to print the cards, we use the str function to get their print representation. Passing an object as an argument to str, i.e. str(c), is equivalent to invoking the __str__ method on the object, i.e. c.__str__() .

Thirdly, we are using the variables s and spaces as accumulators. Initially, s and spaces are empty strings. Each time through the loop, a new string is generated and concatenated to the old value of s to get the new value. Similarly, each time through the loop a single space is added to spaces to increase the indentation level. When the loop ends, s finally contains the complete string representation of the Deck, which looks like this:

>>> red_deck = Deck()
>>> print(red_deck)
Ace of Clubs
 2 of Clubs
  3 of Clubs
   4 of Clubs
     5 of Clubs
       6 of Clubs
        7 of Clubs
         8 of Clubs
          9 of Clubs
           10 of Clubs
            Jack of Clubs
             Queen of Clubs
              King of Clubs
               Ace of Diamonds
                2 of Diamonds
                 ...

And so on. Even though the result appears on 52 lines, it is one long string that contains newlines.

Shuffling the deck

If a deck is perfectly shuffled, then any card is equally likely to appear anywhere in the deck, and any location in the deck is equally likely to contain any card.

To shuffle the deck, we will use the randrange function from the random module. With two integer arguments, a and b, randrange chooses a random integer in the range a <= x < b. Since the upper bound is strictly less than b, we can use the length of a list as the second parameter, and we are guaranteed to get a legal index in the list of cards. For example, if rng has already been instantiated as a random number source, this expression chooses the index of a random card in a deck:

rng.randrange(0, len(self.cards))

An easy way to shuffle the deck is by traversing the cards and swapping each card with a randomly chosen one. It is possible that the card will be swapped with itself, but that is fine. In fact, if we precluded that possibility, the order of the cards would be less than entirely random:

class Deck:
    ...
    def shuffle(self):
        import random
        rng = random.Random()        # Create a random generator
        num_cards = len(self.cards)
        for i in range(num_cards):
            j = rng.randrange(i, num_cards)
            (self.cards[i], self.cards[j]) = (self.cards[j], self.cards[i])

>>> red_deck.shuffle()
>>> print(red_deck)

Rather than assuming that there are fifty-two cards in the deck, we get the actual length of the list and store it in num_cards. This avoids having hardcoded numbers in the code, so that the algorithm is more generic and can be reused easily for other sizes of decks (such as those used for the blackjack card game).

Secondly, rather than looping over all cards, we now use a loop variable i to loop over the range of all cards, and access each card using its index i. We swap the current card at index i with one at a higher index j, chosen randomly from the cards that haven't been shuffled yet. Then we swap the current card (i) with the selected card (j) using a tuple assignment:

(self.cards[i], self.cards[j]) = (self.cards[j], self.cards[i])

While this is a good shuffling method, a random number generator object also has a shuffle method that can shuffle elements in a list, in place. So we could rewrite this function to use the one provided for us:

class Deck:
    ...
    def shuffle(self):
        import random
        rng = random.Random()        # Create a random generator
        rng.shuffle(self.cards)      # Use its shuffle method

Removing and dealing cards

Another method that would be useful for the Deck class is remove, which takes a card as a parameter, removes it and returns True, or False if the card was not in the deck (for example because it already has been removed before):

class Deck:
    ...
    def remove(self, card):
        if card in self.cards:
            self.cards.remove(card)
            return True
        else:
            return False

The in operator returns True if the first operand is in the second. If the first operand is an object, Python uses the object's __eq__ method to determine equality with items in the list. Since the __eq__ we provided in the Card class checks for deep equality, the remove method checks for deep equality.

To deal cards, we want to remove and return the top card. The list method pop provides a convenient way to do that:

class Deck:
    ...
    def pop(self):
        return self.cards.pop()

Actually, pop removes the last card in the list, so we are actually dealing from the bottom of the deck.

One more operation that we are likely to want is the Boolean function is_empty, which returns True if the deck contains no more cards:

class Deck:
    ...
    def is_empty(self):
        return self.cards == []

Glossary

accumulator

A variable used in a loop to accumulate a series of values, such as by concatenating them onto a string or adding them to a running sum.

class attribute

A variable that is defined inside a class definition but outside any method. Class attributes are accessible from any method in the class and are shared by all instances of the class.

class variable

synonym for class attribute

encode

To represent one type of value using another type of value by constructing a mapping between them.

magic methods for relational operators

__eq__ (equals) overloads the == operator

__le__ (equals) overloads the <= operator

__ge__ (equals) overloads the >= operator

__lt__ (equals) overloads the < operator

__gt__ (equals) overloads the > operator

__ne__ (equals) overloads the != operator

References