Table des matières
Objects
Classes and Objects – the Basics
Source: this section is heavily based on Chapter 15 of [ThinkCS] though adapted to better fit with the contents, terminology and notations of this particular course.
Object-oriented programming
Python is an object-oriented programming language, which means that it supports many of the features of the [object_oriented_programming] paradigm.
Object-oriented programming (OOP) has its roots in the 1960s, but it wasn't until the mid 1980s that it became a mainstream [programming_paradigm] used in the creation of new software. It was developed as a way to handle the rapidly increasing size and complexity of software systems, and to make it easier to modify and maintain these large and complex systems over time.
Up to now, most of the programs we have been writing in this course used a [procedural_programming] style. In the procedural programming paradigm the focus is on writing functions or procedures, which operate on data. In object-oriented programming, the focus is on creating objects which group both data and the functions or methods, which operate on that data. We have already seen examples of objects such as turtles and strings. An object definition often corresponds to some object or concept in the real world, and the functions (methods) that operate on (the data encapsulated in) that object correspond to the ways those real-world objects can interact.
User-defined compound data types
Objects are created from classes. Classes describe what methods an object understands and what data it contains. We've already seen classes like str, int, float and Turtle. We are now ready to create our first user-defined class: the Point.
Consider the concept of a mathematical point. In two dimensions, a point can be considered as a pair of two numbers (the point's coordinates) that are treated collectively as a single object. Points are often written in parentheses, with a comma separating the coordinates. For example, (0,0) represents the origin, and (x,y) represents the point x units to the right (or left, if negative) and y units up (or down, if negative) from the origin.
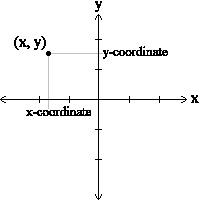
Some of the typical operations that one associates with points might be calculating the distance of a point from the origin, or from another point, or finding a midpoint of two points, or asking if a point falls within a given rectangle or circle. We'll shortly see how we can organise these operations together with the data.
A natural way to represent a point in Python is with two numeric values. The question, then, is how to group these two values into a compound object. The quick and dirty solution is to use a tuple, for example we could write p = (0,0) and q = (1,1), and for some applications that might be a good choice. But we would still need to define dedicated procedures to do something useful with these tuples representing points.
An alternative is to define a new class. This approach involves a bit more effort, but its many advantages will become apparent soon. Since we want each of our points to have an x and a y value, our first class definition looks like this:
class Point: """ The Point class represents and manipulates x,y coordinates. """ def __init__(self): """ Create a new point at the origin """ self.x = 0 self.y = 0
Although class definitions like the one above can appear anywhere in a program, they are usually put near the beginning (after the import statements). Some programmers and languages prefer to put every class in a file or module of its own --- we won't do that for now. The syntax rules for a class definition are the same as for other compound statements. There is a header which begins with the keyword, class, followed by the name of the class, and ending with a colon. Indentation levels tell us where the class ends.
If the first line after the class header is a string, it becomes the [docstring] of the class, and will be recognised by various tools. (This is also the way docstrings work in functions.)
Every class should have an initialiser method which is automatically called whenever a new object (also known as instance) of that class is created (in what follows we will use the terms object and instance interchangeably). This initialiser method has a special name __init__ (with a double underscore character before and after the name). For the class Point, the __init__ method sets the x and y coordinates of the created object to zero. In general, the __init__ method gives a programmer the opportunity to set up the attributes required within a new instance of the class by giving them their initial state/values. The self parameter (we could choose any other name, but self is the convention) is automatically set to reference the newly created object that needs to be initialised. So, for example, self.x = 0 will assign the value of 0 to the x attribute of the newly created point object itself.
We can use our new Point class now to create two Point objects:
p = Point() # Instantiate an object of type Point q = Point() # Make a second point object print(p.x, p.y, q.x, q.y) # Each point object has its own x and y
This program prints:
0 0 0 0
because during the initialisation of the objects p and q, we created two attributes called x and y for each, and gave them both the value 0.
This way of creating objects should look familiar to you. We've used classes before to create multiple Turtle objects:
from turtle import Turtle tess = Turtle() # Instantiate an object of type Turtle alex = Turtle() # Instantiate a second object of type Turtle
The variables p and q above are assigned references to two new Point objects. A function like Turtle() or Point() that creates a new object instance from its corresponding class is called a constructor. Every class automatically provides a constructor function which is named the same as the class.
It may be helpful to think of a class as a factory for making objects. The class itself isn't an instance of a point, but it contains the machinery to make point instances. Every time we call the constructor, we're asking the factory to make us a new object. As the object comes off the production line, its initialisation method is executed to get the object properly set up with its default factory settings.
The combined process of "construct me a new object" and "get its settings initialised to the factory default settings" is called instantiation.
Attributes
Object instances have both attributes (the data contained in the instance) and methods (the operations that act on that data). Whereas the methods are the same for all objects of a same class (we will see in a next section how to define such methods), the attribute values are specific to each particular instance of that class. For that reason, the attributes are sometimes also referred to as instance variables. Of course, initially they are initialised to the same factory default settings, but once an object has been created, we can modify its attribute values by using the following dot notation:
>>> p.x = 3 >>> p.y = 4
This sets the x attribute of the object instance p to the value 3 and its y attribute to the value 4.
Both modules and instances create their own namespaces, and the syntax for accessing names contained in each, called attributes, is the same. In this case the attribute we are selecting is a data item from an instance.
The following memory diagram shows the result of these assignments:
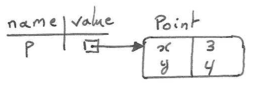
The variable p refers to a Point object, which contains two attributes x and y. Each attribute contains a number.
We can access the value of an attribute using the same syntax:
>>> print(p.y) 4 >>> x = p.x >>> print(x) 3
The expression p.x means, "Go to the point object that p refers to and get the value of its attribute named x". In this case, we assign that value to a global variable named x. There is no conflict between the variable named x (in the global namespace) and the attribute named x (in the namespace belonging to the instance). The purpose of the dot notation is to fully qualify which variable we are referring to unambiguously.
We can use dot notation as part of any expression, so the following statements are legal:
print("(x={0}, y={1})".format(p.x, p.y)) distance_from_origin = pow(p.x * p.x + p.y * p.y,1/2) print(distance_from_origin)
The first line outputs (x=3, y=4). (Note that the first line is equivalent to writing print("(x="+str(p.x)+", y="+str(p.y)+")") but uses the [format] method which supports advanced string formatting.) The second line calculates the value 5. The third line prints this calculated value.
Improving the initialiser
To create a new point object at position (7, 6) we currently need three lines of code:
p = Point() # Create a new instance of class Point p.x = 7 # Set its x attribute to the value 7 p.y = 6 # Set its y attribute to the value 6
We can make our class constructor more general by placing extra parameters into the __init__ method, as shown in this example:
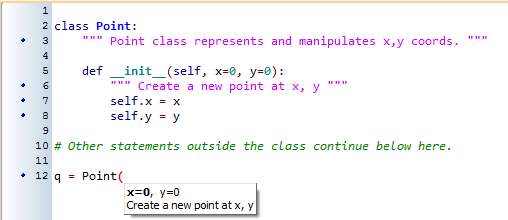
class Point: """ The Point class represents and manipulates x,y coordinates. """ def __init__(self, x=0, y=0): """ Create a new point at coordinates x, y. @pre: x and y are numbers (if not supplied, the number 0 will be used) @post: the attributes x and y of this point instance have been initialised to the values x and y passed as arguments """ self.x = x self.y = y # Other statements outside the class continue below here.
The x and y parameters here are both optional. If the caller does not supply any arguments for x and y, they'll get the default values of 0. Here is our improved class in action:
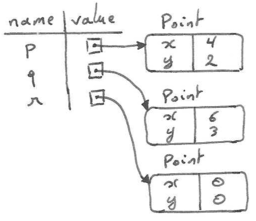
>>> p = Point(4, 2) >>> q = Point(6, 3) >>> r = Point() # r represents the origin (0, 0) >>> print(p.x, q.y, r.x) 4 3 0
Below you can find another memory diagram depicting the three objects that have been created in the computer's memory.
Technically speaking ...
If we are really fussy, we would argue that the __init__ method's docstring is inaccurate. Indeed, __init__ doesn't create the object (i.e. set aside memory for it; it's the constructor that does that), --- it just initialises the object to its factory-default settings after its creation.
But programming tools like for example PyScripter understand that instantiation --- creation and initialisation --- happen together, and they choose to display the initialiser's docstring as the tooltip to guide the programmer that calls the class constructor.
So we're writing the docstring so that it makes the most sense when it pops up to help the programmer who is using our Point class:
Adding other methods to the class
The key advantage of using a class like Point rather than a simple tuple (6, 7) now becomes apparent. We can add methods to the Point class that are sensible operations for points, but which may not be appropriate for other tuples like (25, 12) which might represent, say, a day and a month, e.g. Christmas day. So being able to calculate the distance from the origin is sensible for points, but not for (day, month) data. For (day, month) data, we'd like different operations, perhaps to find what day of the week it will fall on in 2050.
Creating a class like Point brings an exceptional amount of "organisational power" to our programs, and to our thinking. We can group together the sensible operations, and the kinds of data they apply to, and each instance of the class can have its own individual state.
A method behaves like a function except that it is invoked on a specific instance, e.g. t.right(90) which turns a Turtle object t 90 degrees to the right. Like data attributes, methods are accessed using the dot notation.
instance methods versus class methods
Technically speaking, there exist two kinds of methods in Python: instance methods, which can be invoked on specific instances (i.e., objects), and class methods, which can be invoked on a class itself without having to create an instance of that class first. Since most of the methods you will encounter will be instance methods, for now, when we use the term method, we mean instance method. We will not explain the notion of class methods yet, in order not to confuse you more than necessary.
Let's add another method, distance_from_origin, to our class Point to see better how methods work:
class Point: """ The Point class represents and manipulates x,y coordinates. """ def __init__(self, x=0, y=0): """ Create a new point at coordinates x, y. @pre: x and y are numbers (if not supplied, the number 0 will be used) @post: the attributes x and y of this point instance have been initialised to the values x and y passed as arguments """ self.x = x self.y = y def distance_from_origin(self): """ Compute my distance from the origin @pre: - @post: returns the Euclidian distance of this point to the origin (0,0) """ return pow((self.x ** 2) + (self.y ** 2),1/2)
When defining a method, it must always have a first parameter that refers to the instance being manipulated, i.e. the object itself. For that reason it is customary to name this parameter self.
Now let's create a few point instances, look at their attributes, and call our new distance calculation method on them. (Note that we must execute our new class definition above first, to make our modified Point class available to the interpreter.)
>>> p = Point(3, 4) >>> p.x 3 >>> p.y 4 >>> p.distance_from_origin() 5.0 >>> q = Point(5, 12) >>> q.x 5 >>> q.y 12 >>> q.distance_from_origin() 13.0 >>> r = Point() >>> r.x 0 >>> r.y 0 >>> r.distance_from_origin() 0.0
Notice that, although the method distance_from_origin(self) was defined with a first parameter self, the caller of distance_from_origin() does not explicitly supply an argument to match this self parameter; nevertheless this parameter will be bound to self automatically, behind our back. Remember that: when you define a method in a class you should add a first parameter self representing the instance being manipulated; when calling the method you should drop that parameter, it will be filled in automatically behind your back.
Instances as arguments and parameters
We can pass any object as an argument in the usual way. We've already seen this in some of the turtle examples, where we passed the turtle to some function, so that the function could control and use whatever turtle instance we passed to it. Be aware that a variable only holds a reference to an object, so passing a turtle object into a function creates an alias: both the caller and the called function now have a reference to that turtle, but there is only one turtle!
Here is a simple function involving our new Point objects:
def print_point(pt): print("({0}, {1})".format(pt.x, pt.y))
print_point takes a point as argument and formats the output in whichever way we choose. If we call print_point(p) with point p as defined previously, the output is (3, 4).
Converting an instance to a string
However, an object-oriented programmer would not do what we've just done with print_point. Rather than having a globally defined print function outside of the class definition, when working with classes and objects, a preferred alternative is to add a new method to the class definition. And we don't like chatterbox methods that call print. A better approach is to have a method so that every instance can produce a string representation of itself. This string representation can then easily be printed from the outside. Let's call this method that produces a string representation of an object to_string:
class Point: # ... same as before ... def to_string(self): return "({0}, {1})".format(self.x, self.y)
Again, observe how the method to_string takes a parameter self as first argument. Also observe how the point's attributes are accessed within that method by referring to self using the dot notation.
(As a reminder, the statement "({0}, {1})".format(self.x, self.y) is equivalent to writing "("+str(self.x)+", "+str(self.y)+")".)
Now we can say:
>>> p = Point(3, 4) >>> print(p.to_string()) (3, 4)
But doesn't there already exist a str type converter that can turn an object into a string? Yes! And doesn't print automatically use this when printing things? Yes again! But these automatic mechanisms do not (yet) seem to do exactly what we want:
>>> str(p) '<__main__.Point object at 0x01F9AA10>' >>> print(p) '<__main__.Point object at 0x01F9AA10>'
Rather than printing the contents of the object they print a unique reference to the object.
Luckily Python has a clever trick to fix this. If we call our new method __str__ (with a double underscore character before and after the method name) instead of to_string, the Python interpreter will use our code instead of the default str function whenever it needs to convert a Point to a string. Let's re-do this again, now:
class Point: # ... same as before ... def __str__(self): # All we have done is renamed the method return "({0}, {1})".format(self.x, self.y)
and now things are looking great!
>>> str(p) # Python now magically uses the __str__ # method that we wrote. (3, 4) >>> print(p) (3, 4)
Such special methods like __str__ (and also the __init__ method introduced before) are called [magic_methods] in Python. Typically, whenever you define your own new classes, you may want to implement such an __str__ method on them, to be able to easily inspect objects of those classes by printing them.
Instances as return values
Functions and methods can return object instances. For example, given two Point objects, find their midpoint. First we'll write this as a regular function:
def midpoint(p1, p2): """ @pre: p1 and p2 are instances of class Point @post: returns the midpoint of points p1 and p2 """ mx = (p1.x + p2.x)/2 my = (p1.y + p2.y)/2 return Point(mx, my)
This function creates and returns a new Point object:
>>> p = Point(3, 4) >>> q = Point(5, 12) >>> r = midpoint(p, q) >>> print(r) (4.0, 8.0)
However, as mentioned before, an object-oriented programmer would prefer to define this as a method defined on the class, rather than as a globally defined function. So, let us try to write this function as a method instead. Suppose we have a point object, and wish to find the midpoint halfway between itself and some other target point:
class Point: # ... def halfway(self, target): """ @pre: target is an instance of class Point @post: returns a new instance of class Point representing the halfway point between myself and the target """ mx = (self.x + target.x)/2 my = (self.y + target.y)/2 return Point(mx, my)
This method is almost identical to the function, aside from some renaming. It's usage might be like this:
>>> p = Point(3, 4) >>> q = Point(5, 12) >>> r = p.halfway(q) >>> print(r) (4.0, 8.0)
While this example assigns each point to a variable, this need not be done. Just as function calls are composable, method calls and object instantiation are also composable, leading to this alternative that uses no variables:
>>> print(Point(3, 4).halfway(Point(5, 12))) (4.0, 8.0)
A change of perspective
The original syntax for a function call, print_time(current_time), suggests that the function is the active agent. It says something like, "Hey, print_time! Here's an object for you to print."
In object-oriented programming, objects are considered the active agents instead. An invocation like current_time.print_time() says "Hey current_time! Please print yourself!"
In our early introduction to turtles, we used an object-oriented style, so that we said t.forward(100), which asks the turtle t to move itself forward by the given number of steps.
This change in perspective might be more polite, but it may not initially be obvious that it is useful. But sometimes shifting responsibility from the functions onto the objects makes it possible to write more versatile functions, and makes it easier to maintain and reuse code.
The most important advantage of the object-oriented style is that it fits our mental chunking and real-life experience more accurately. In real life our cook method is part of our microwave oven --- we don't have a cook function sitting in the corner of the kitchen, into which we pass the microwave! Similarly, we use the cellphone's own methods to send an sms, or to change its state to silent. The functionality of real-world objects tends to be tightly bound up inside the objects themselves. [object_oriented_programming] allows us to accurately mirror this when we organise our programs.
Objects can have state
Objects are most useful when we also need to keep some state that is updated from time to time. Consider a turtle object. Its state consists of things like its position, its heading, its colour, and its shape. A method like left(90) updates the turtle's heading, forward changes its position, and so on.
For a bank account object, a main component of the state would be the current balance, and perhaps a log of all transactions. The methods would allow us to query the current balance, deposit new funds, or make a payment. Making a payment would include an amount, and a description, so that this could be added to the transaction log. We'd also want a method to show the transaction log.
Glossary
- attribute
- One of the named data items that makes up an object. Another word for attribute is instance variable.
- class
- A user-defined compound type. A class can also be thought of as a template or factory for the objects that are instances of it.
- constructor
- A class can also be seen as a "factory" for making objects of a certain kind. Every class thus provides a constructor method, called by the same name as the class, for making new instances of this kind. If the class has an initialiser method, this method is used to get the attributes (i.e. the state) of the new instance properly set up.
- initialiser method
- A special method in Python (called __init__) that is invoked automatically to set a newly created object's attributes to their initial (factory-default) state.
- instance
- An object whose type is of some class. The words instance and object are used interchangeably.
- instance variable
- Since the attribute values of an object are specific to that particular object (i.e., another object of the same class may have another value for that attribute), they are sometimes also referred to as instance variables.
- instantiate
- To create an instance of a class, and to run its initialiser method.
- instance method
- A function that is defined inside a class definition and is invoked on instances of that class.
- magic method
- Magic methods are special methods like __init__ or __str__ that you can define to add some magic to your classes. For example Python magically knows that when a new object gets constructed it should call the __init__ method to initialise the attributes of the newly created object, or that when you print an object, it should call the __str__ method to get a printable string representation of the object. Magic methods are always surrounded by double underscores.
- method
- If it is clear from the context we will often refer to an instance method simply as a method. (We will learn later that there is also such a thing as class methods, which is not the same as instance methods.)
- object
- A compound data type that is often used to model a thing or concept in the real world. It bundles together the data and the operations that are relevant for that kind of data. The words instance and object are used interchangeably.
- object-oriented programming
- A powerful style of programming in which data and the operations that manipulate it are organized into objects.
- object-oriented language
- A language that provides features, such as user-defined classes and inheritance, that facilitate object-oriented programming.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
| [object_oriented_programming] | (1, 2) http://en.wikipedia.org/wiki/Object-oriented_programming |
| [programming_paradigm] | http://en.wikipedia.org/wiki/Programming_paradigm |
| [procedural_programming] | http://en.wikipedia.org/wiki/Procedural_programming |
| [magic_methods] | https://rszalski.github.io/magicmethods/ |
| [docstring] | https://www.python.org/dev/peps/pep-0257/ |
| [format] | https://www.python.org/dev/peps/pep-3101/#id16 |
Classes and Objects – Digging a little deeper
Source: this section is heavily based on Chapter 16 of [ThinkCS] though adapted to better fit with the contents, terminology and notations of this particular course.
Rectangles
Suppose we want a class to represent rectangles located somewhere in the Cartesian X-Y plane. What information do we have to provide in order to specify such a rectangle? To simplify things, let us assume that the rectangle is always oriented either vertically or horizontally, never at an angle.
There are a few possibilities: we could specify the center of the rectangle (two coordinates) and its size (width and height); or we could specify one of the corners and the size; or we could specify two opposing corners. A conventional choice is to specify the upper-left corner of the rectangle, and its size.
As with the Point class before, we'll define a new class Rectangle, and provide it with an initialiser method __init__ and a string converter method __str__. Also don't forget to always add as first parameter to your methods a reference to self.
class Rectangle: """ The Rectangle class represents rectangles in a Cartesian plane. """ def __init__(self, pos, w, h): """ Create a new rectangle with upper-left corner at point pos, with width w and height h. @pre: pos is an instance of class Point width and height are positive numbers @post: the attributes corner, width and height of this rectangle instance have been initialised to the values pos, w and h passed as arguments """ self.corner = pos self.width = w self.height = h def __str__(self): """ @pre: - @post: returns a string representation of this rectangle in the following format ((x, y), width, height) where width and height are the values of the corresponding attributes of this object and x and y are the corresponding attributes of the point object stored in the corner attribute """ return "({0}, {1}, {2})".format(self.corner, self.width, self.height) box = Rectangle(Point(0, 0), 100, 200) bomb = Rectangle(Point(100, 80), 5, 10) # In some video game print("box: ", box) print("bomb: ", bomb)
Note how, to specify the upper-left corner, we embedded a Point object (as was defined in the previous section) within our new Rectangle object. We create two new Rectangle objects, and then print them, which produces:
box: ((0, 0), 100, 200) bomb: ((100, 80), 5, 10)
The dot operator can be composed (chained). For example, the expression box.corner.x means: "Go to the object that box refers to, select its attribute named corner, then go to that object and select its attribute named x".
The figure below shows the state of this object:
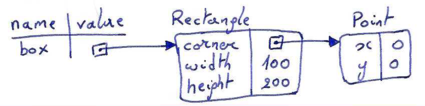
From the figure it can easily be seen that printing box.corner.x would produce:
>>> print(box.corner.x) 0
When reasoning about the state of objects (their attributes and the values they contain), we strongly encourage you to draw such memory diagrams.
Objects are mutable
We can change the state of an object by making an assignment to one of its attributes. For example, to grow the size of a rectangle without changing its position, we could modify the values of its width and height attributes:
box.width += 50 box.height += 100
The memory diagram below sketches the effect of making these modifications (in green):
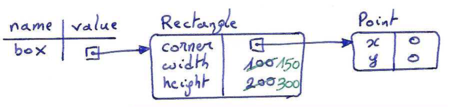
After this, print("box: ", box) produces as output:
box: ((0, 0), 150, 300)
However, we prefer to provide a method to encapsulate this state change operation inside the class. We will also provide another method to move the position of the rectangle over a certain distance:
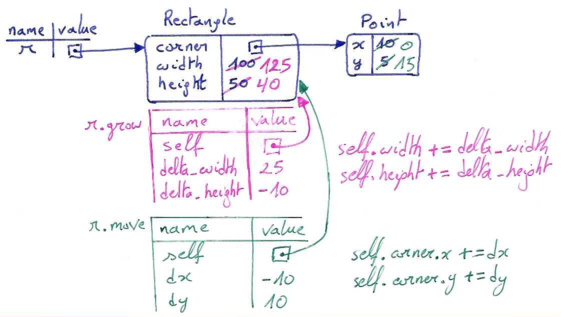
class Rectangle: # ... same as before ... def grow(self, delta_width, delta_height): """ Grow (or shrink) this rectangle by the deltas @pre: delta_width and delta_height are (positive or negative) numbers @post: this rectangle's width was grown to its original width plus delta_width (or shrunk in case delta_width is negative); this rectangle's height was grown to its original height plus delta_height (or shrunk in case delta_height is negative); nothing is returned """ self.width += delta_width self.height += delta_height def move(self, dx, dy): """ Move this object by the given distances @pre: dx and dy are (positive or negative) numbers @post: the x-coordinate of this rectangle's corner was moved from its original position x to x plus dx (moved right if dx is positive or moved left if dx is negative); the y-coordinate of this rectangle's corner was moved from its original position y to y plus dy (moved down if dy is positive or moved up if dy is negative); nothing is returned """ self.corner.x += dx self.corner.y += dy
Let us try this:
>>> r = Rectangle(Point(10,5), 100, 50) >>> print(r) ((10, 5), 100, 50) >>> r.grow(25, -10) >>> print(r) ((10, 5), 125, 40) >>> r.move(-10, 10) print(r) ((0, 15), 125, 40)
Again, a memory diagram may help you to better visualise how the state of the rectangle and point objects get modified (the part in blue corresponds to the definition of the rectangle object, in pink the effect of growing it, in green the effect of moving it):
Sameness
The meaning of the word "same" seems perfectly clear until we give it some thought, and then we realize there is more to it than we initially expected.
For example, if we say, "Alice and Bob have the same mother", we mean that her mother and his are the same person. If we say, however, "Alice and Bob have the same car", we probably mean that her car and his are the same make and model, but that they are two different cars. But if we say, "Alice and Bob share the same car", we probably mean that they actually share the usage of a single car.
When we talk about objects, there is a similar ambiguity. For example, if two Points are the same, does that mean they are two point objects that contain the same data (coordinates) or that they are actually the same object?
We can use the is operator to find out if two references refer to the same object:
>>> p1 = Point(3, 4) >>> p2 = Point(3, 4) >>> p1 is p2 False
In this example, even though p1 and p2 contain the same coordinates, they are not the same object. If we assign the value of p1 to a new variable named p3, however, then the two variables are aliases of (refer to) the same object:
>>> p3 = p1 >>> p1 is p3 True
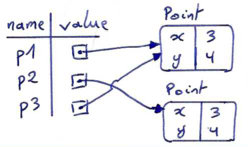
This type of equality is called shallow equality because it compares only the references, not the actual contents of the objects' attributes. With the is operator, two things are considered the same only if they refer to the exact same thing. This means that even the following comparison would yield False:
>>> Point(3, 4) is Point(3, 4) False
The reason is that whenever you call the Point(3, 4) constructor you create a new distinct point object that happens to have the values 3 and 4 for its x and y coordinates. But the two objects are distinct and stored in different memory locations.
To compare the contents of the objects — deep equality — we can write a function called same_coordinates:
def same_coordinates(p1, p2): """ @pre: p1 and p2 are instances of class Point @post: returns True if both the x attribute of p1 and p2 are equal and their y attributes are equal; returns False otherwise """ return (p1.x == p2.x) and (p1.y == p2.y)
Now if we try to run the comparisons above again, but using same_coordinates as a comparator rather than the is operator, we can see that they are all considered the same:
>>> same_coordinates(p1, p2) True >>> same_coordinates(p1, p3) True >>> same_coordinates(Point(3, 4),Point(3, 4)) True
Of course, if two variables refer to the same object (as is the case with p1 and p3), they have both shallow and deep equality.
Beware of ==
Python has a powerful feature that allows a designer of a class to decide what an operation like == or < should mean. We'll cover that in more detail later, but the principle is the same as how we can control how our own objects are converted to strings, as was illustrated in the previous section with the magic method __str__. But sometimes the language implementors will attach a shallow equality semantics to ==, and sometimes deep equality, as shown in this little experiment:
p1 = Point(4, 2) p2 = Point(4, 2) print("== on Points returns", p1 == p2) # By default, == on Point objects does a SHALLOW equality test l1 = [2,3] l2 = [2,3] print("== on lists returns", l1 == l2) # But by default, == does a DEEP equality test on lists
This outputs:
== on Points returns False == on lists returns True
So we conclude that even though the two lists (or tuples, etc.) are distinct objects with different memory addresses, for lists the == operator tests for deep equality, while in the case of points it makes a shallow test.
Copying
Aliasing (different variables referring to a same object) can make a program difficult to read because changes made in one place might have unexpected effects in another place. It is hard to keep track of all the variables that might refer to a given object.
Copying an object is often an alternative to aliasing. The copy module contains a function called copy that can duplicate any object:
>>> import copy >>> p1 = Point(3, 4) >>> p2 = copy.copy(p1) >>> p1 is p2 False >>> same_coordinates(p1, p2) True
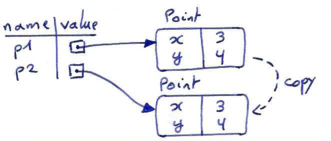
Once we import the copy module, we can use the copy function to make a new Point. p1 and p2 are not a reference to the same object, but they are distinct point objects that contain the same data. p2 is a newly created object of which the data is copied from p1.
To copy a simple object like a Point, which doesn't contain any embedded objects, using the copy function suffices, even though it only performs a shallow copying.
For something like a Rectangle object, which contains an internal reference to a Point object (to represent its upper-left corner), a simple shallow copy wouldn't suffice however. It would create a new Rectangle object, copying the values of the width and height attributes of the original Rectangle object. But for the corner attribute it would simply copy the reference to the Point object it contains, so that both the old and the new Rectangle's corner attribute would refer to the same Point.
>>> import copy >>> b1 = Rectangle(Point(0, 0), 100, 200) >>> b2 = copy.copy(b1)
If we create a rectangle b1 in the usual way, and then make a copy b2, using copy, the resulting memory diagram looks like this:
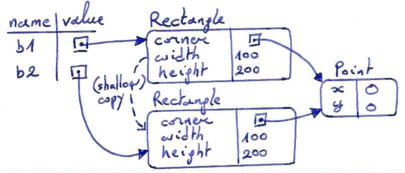
This is almost certainly not what we want. In this case, invoking grow on one of the Rectangle objects would not affect the other (since the grow method only acts on the width and height attributes which were copied), but invoking move on either Rectangle object would affect the other! That would be very weird, since the rectangles would share their upper-left corner but not their size attributes.
>>> b1.move(10,10) >>> print(b2.corner) (10,10)
In the example above, although we didn't explicitly move b2, we can see that its corner object has changed as a side-effect of moving b1. This behavior is confusing and error-prone. The problem is that the shallow copy of the rectangle object has created an alias to the Point that represents the corner, rather than making a copy of that point.
Fortunately, the copy module also contains a function named deepcopy that copies not only the object but also any embedded objects (recursively). It won't be surprising to learn that this operation is called a deep copy.
>>> b1 = Rectangle(Point(0, 0), 100, 200) >>> b2 = copy.deepcopy(b1) >>> b1.move(10,10) >>> print(b1.corner) (10,10) >>> print(b2.corner) (0,0)
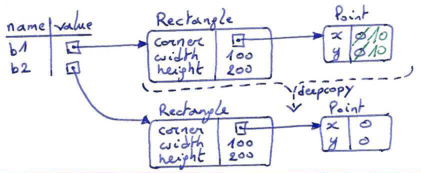
Now b1 and b2 are completely separate objects.
Glossary
- deep copy
- To copy the contents of an object as well as any embedded objects, and any objects embedded in them, and so on; implemented by the deepcopy function in the copy module.
- deep equality
- Equality of values, or two references that point to (potentially different) objects that have the same attribute values.
- shallow copy
- To copy the contents of an object, including any references to embedded objects; implemented by the copy function in the copy module.
- shallow equality
- Equality of references, or two references that point to the same object.
- string converter method
- A magic method in Python (called __str__) that produces an informal string representation of an object. For example, this is the string that will be printed when calling the print function on that object.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Even more object-oriented programming
Source: this section is heavily based on the first half of Chapter 21 of [ThinkCS] though adapted to better fit with the contents, terminology and notations of this particular course.
Now that we've seen the basics of object-oriented programming and have created our own first Point and Rectangle classes, let's take things yet a step further.
MyTime
As another example of a user-defined class, we'll define a class called MyTime that records the time of day. We provide an __init__ method to ensure that every instance is created with appropriate attributes and initialisation. The class definition looks like this:
class MyTime: def __init__(self, hrs=0, mins=0, secs=0): """ @pre: hrs, mins, secs are positive integers; 0 <= mins < 60, 0 <= secs < 60; if not supplied a default value of 0 is used @post: the attributes hours, minutes and seconds of this MyTime object have been initialised to hrs, mins, secs (or 0 if no values were supplied) """ self.hours = hrs self.minutes = mins self.seconds = secs
We can then create and instantiate a new MyTime object by calling the constructor with the necessary arguments for the initialisation method:
tim1 = MyTime(11, 59, 30)
The memory diagram for this object looks like this:
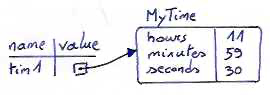
We leave it as an exercise for the reader (please do it!) to also add a __str__ method so that MyTime objects can print themselves decently. For example, the object above should print as 11:59:30. (If you don't know how to do this, look at the Rectangle class of the previous chapter for inspiration.)
Pure functions
In the next few sections, we'll write two versions of a function called add_time, which calculates the sum of two MyTime objects. They will demonstrate two kinds of functions: pure functions and modifiers.
The following is a first rough version of add_time:
def add_time(t1, t2): """ @pre: t1 and t2 are instances of class MyTime @post: a new MyTime object is returned of which the hours, minutes and seconds attributes are the sum of the respective attributes in t1 and t2 """ h = t1.hours + t2.hours m = t1.minutes + t2.minutes s = t1.seconds + t2.seconds sum_t = MyTime(h, m, s) return sum_t
The function creates a new MyTime object and returns a reference to the new object. This is called a pure function because it does not modify any of the objects passed to it as parameters and it has no side effects, such as updating global variables, displaying a value, or getting user input.
Here is an example of how to use this function. We'll create two MyTime objects: current_time, which contains the current time; and bread_time, which contains the amount of time it takes for a breadmaker to make bread. Then we'll use add_time to figure out when the bread will be done.
>>> current_time = MyTime(9, 14, 30) >>> bread_time = MyTime(3, 35, 0) >>> done_time = add_time(current_time, bread_time) >>> print(done_time) 12:49:30
The output of this program is 12:49:30, which is correct. On the other hand, there are cases where the result is not correct. Can you think of one?
The problem is that this function does not deal with cases where the number of seconds or minutes adds up to more than sixty. When that happens, we have to carry the extra seconds into the minutes column or the extra minutes into the hours column.
Here's an improved version of the function. (We left out its specification, because it would get pretty big and we will soon propose a better alternative solution.)
def add_time(t1, t2): h = t1.hours + t2.hours m = t1.minutes + t2.minutes s = t1.seconds + t2.seconds if s >= 60: s -= 60 m += 1 if m >= 60: m -= 60 h += 1 sum_t = MyTime(h, m, s) return sum_t
This function is already starting to get bigger, and still doesn't work for all possible cases. Later we will suggest an alternative approach that yields better code.
Modifiers
There are times when it is useful for a function to modify one or more of the objects it gets as parameters. Usually, the caller keeps a reference to the objects it passes, so any changes the function makes are visible to the caller. Functions that work this way are called modifiers.
For example, increment, which adds a given number of seconds to a MyTime object, when written as a modifier, could behave like this:
>>> t = MyTime(10,20,30) >>> increment(t,70) >>> print(t) 10:21:40
A rough draft of the implementation of this function looks like this:
def increment(t, secs): """ @pre: t is an instance of MyTime; secs is a positive integer @post: the seconds attribute of t is modified by adding secs; if the amount of seconds in t becomes > 60, each surplus of 60 seconds spills over to an extra minute added to the minutes attribute of t; if the amount of minutes in t becomes > 60, each surplus of 60 minutes spills over to an extra hour added to the hours attribute of t; nothing is returned """ t.seconds += secs if t.seconds >= 60: t.seconds -= 60 t.minutes += 1 if t.minutes >= 60: t.minutes -= 60 t.hours += 1
The first line performs the basic operation; the remainder deals with the special cases we saw before.
Note that this function has no return statement nor does it need to create a new object. It simply modifies the state of the Time object t that was passed as first parameter to the function.
Is this function correct? What happens if the parameter secs is much greater than sixty? In that case, it is not enough to carry once; we have to keep doing it until t.seconds is less than sixty. One solution is to replace the if statements with while statements:
def increment(t, secs): # SAME SPECIFICATION AS BEFORE t.seconds += secs while t.seconds >= 60: t.seconds -= 60 t.minutes += 1 while t.minutes >= 60: t.minutes -= 60 t.hours += 1
This function is now correct when seconds is not negative, but it is still not a particularly good nor efficient solution.
>>> t = MyTime(10,20,30) >>> increment(t,100) >>> print(t) 10:22:10
Converting increment to a method
Once again, since object-oriented programmers would prefer to put functions that work with MyTime objects directly into the MyTime class, let's convert increment to a method. To save space, we will leave out previously defined methods in that class, but you should keep them in your version:
class MyTime: # Previous method definitions here... def increment(self, seconds): # SAME SPECIFICATION AS BEFORE self.seconds += seconds while self.seconds >= 60: self.seconds -= 60 self.minutes += 1 while self.minutes >= 60: self.minutes -= 60 self.hours += 1
The transformation is purely mechanical: we move the definition into the class definition and change the name of the first parameter (and all occurrences of that parameter in the method body) to self, to fit with Python style conventions.
Now we can invoke increment using the dot syntax for invoking a method, instead of writing increment(current_time,500) :
>>> current_time = MyTime(11, 58, 30) >>> current_time.increment(500) >>> print(current_time) 12: 6:50
The object current_time on which the method is invoked gets assigned to the first parameter, self. The second parameter, seconds gets the value 500.
An "Aha!" moment
An "Aha!" moment is that moment or instant at which the solution to a problem suddenly becomes clear. Often a high-level insight into a problem can make the programming much easier.
A three-digit number in base 10, for example the number 284, can be represented by 3 digits, the right most one (4) representing the units, the middle one (8) representing the tens, and the left-most one representing the hundreds. In other words, 284 = 2*100 + 8*10 + 4*1.
Our "Aha!" moment consists of the insight that a MyTime object is actually a three-digit number in base 60 ! The "seconds" correspond to the units, the "minutes" to the sixties, and the hours to the thirty-six hundreds. Indeed, 12h03m30s corresponds to 12*3600 + 3*60 + 30 = 43410 seconds.
When we were writing the add_time and increment functions and methods, we were effectively doing addition in base 60, which explains why we had to carry over remaining digits from one column to the next.
This observation suggests another approach to the entire problem --- we can convert a MyTime object into a single number (in base 10, representing the seconds) and take advantage of the fact that the computer knows how to do arithmetic with numbers. The following method can be added to the MyTime class to convert any instance into a corresponding number of seconds:
class MyTime: # ... def to_seconds(self): """ @pre: - @post: returns the total number of seconds represented by this instance of MyTime """ return self.hours * 3600 + self.minutes * 60 + self.seconds
>>> current_time = MyTime(11, 58, 30) >>> seconds = current_time.to_seconds() >>> print(current_time) 11:58:30 >> print(seconds) 43110
Now, all we need is a way to convert from an integer, representing the time in seconds, back to a MyTime object. Supposing we have tsecs seconds, some integer division and modulus operators can do this for us:
hrs = tsecs // 3600 leftoversecs = tsecs % 3600 mins = leftoversecs // 60 secs = leftoversecs % 60
You might have to think a bit to convince yourself that this technique to convert from one base to another is correct. Remember that the // operator represents integer division and that the modulus operator % calculates the remainder of integer division.
As mentioned in the previous sections, one of the main goals of object-oriented programming is to wrap together data with the operations that apply to it. So we'd like to put the above conversion logic inside the MyTime class. A good solution is to rewrite the class initialisation method __init__ so that it can cope with initial values of seconds or minutes that are outside the normalised values. (A normalised time would be something like 3 hours 12 minutes and 20 seconds. The same time, but unnormalised could be 2 hours 70 minutes and 140 seconds, where the minutes or seconds are more than the expected maximum of 60.)
Let's rewrite a more powerful initialiser for MyTime:
class MyTime: # ... def __init__(self, hrs=0, mins=0, secs=0): """ Create a new MyTime object initialised to hrs, mins, secs. @pre: hrs, mins, secs are positive integers; if not supplied a default value of 0 is used @post: the attributes hours, minutes and seconds of this MyTime object have been initialised to hrs, mins, secs (or 0 if no values were supplied) In case the values of mins and secs are outside the range 0-59, the resulting MyTime object will be normalised, so that they are in this range """ # Calculate the total number of seconds to represent totalsecs = hrs*3600 + mins*60 + secs self.hours = totalsecs // 3600 # Split in h, m, s leftoversecs = totalsecs % 3600 self.minutes = leftoversecs // 60 self.seconds = leftoversecs % 60
Now we can rewrite add_time like this:
def add_time(t1, t2): """ @pre: t1 and t2 are instances of class MyTime @post: a new MyTime object is returned of which the total time in seconds is the sum of the total time in seconds of t1 and t2 """ secs = t1.to_seconds() + t2.to_seconds() return MyTime(0, 0, secs)
This version is much shorter than the original, and it is much easier to demonstrate or reason that it is correct. Notice that we didn't have to do anything for carrying over seconds or minutes that are too large; that is handled automatically by our new initialiser method now. (Isn't that just wonderful?)
>>> current_time = MyTime(9, 14, 30) >>> bread_time = MyTime(3, 35, 0) >>> done_time = add_time(current_time, bread_time) >>> print(done_time) 12:49:30
Note that we could also implement add_time as a method defined on the class MyTime rather than as a globally defined function, but we will leave that to the next chapter.
The final question that remains now is how we can rewrite the increment method that we wrote before, without having to reimplement the logic that we now put into our new initialiser method. The answer to this question is in the question. What if we simply try to call the __init__ method from within the increment method so as to reuse its logic. This can be done surprisingly easily:
def increment(self, secs): """ @pre: t is an instance of MyTime; secs is a positive integer @post: the seconds attribute of t is modified by adding secs; if necessary t gets normalized so that neither the amount of seconds in t nor the amount of minutes in t becomes > 60; nothing is returned """ self.__init__(self.hours,self.minutes,self.seconds+secs)
Again, the carrying over of seconds or minutes that are too large is handled automatically by the initialiser method. It is important to observe that, as opposed to the add_time method, we are not creating a new MyTime object here. We are simply calling __init__ to assign a new state to the existing instance (self).
>>> current_time = MyTime(11, 58, 30) >>> current_time.increment(500) >>> print(current_time) 12: 6:50
Generalisation
In some ways, converting from base 60 to base 10 and back is harder than just dealing with time. Base conversion is more abstract; our intuition for dealing with time is better.
However, if we have the insight to treat time objects as base 60 numbers and make the investment of writing the conversions, we get a program that is shorter, easier to read and debug, and more reliable.
It is also easier to add features later. For example, imagine subtracting two MyTime objects to find the duration between them. The naive approach would be to implement subtraction with borrowing. Using the conversion functions would be easier and more likely to be correct.
Ironically, sometimes making a problem harder (or more general) makes the programming easier, because there are fewer special cases and fewer opportunities for error.
Specialisation versus Generalisation
Computer Scientists are generally fond of specialising their types, while mathematicians often take the opposite approach, and generalise everything.
What do we mean by this?
If we ask a mathematician to solve a problem involving weekdays, days of the century, playing cards, time, or dominoes, their most likely response is to observe that all these objects can be represented by integers. Playing cards, for example, can be numbered from 0 to 51. Days within the century can be numbered. Mathematicians will say "These things are enumerable --- the elements can be uniquely numbered (and we can reverse this numbering to get back to the original concept). So let's number them, and confine our thinking to integers. Luckily, we have powerful techniques and a good understanding of integers, and so our abstractions --- the way we tackle and simplify these problems --- is to try to reduce them to problems about integers."
Computer scientists tend to do the opposite. We will argue that there are many integer operations that are simply not meaningful for dominoes, or for days of the century. So we'll often define new specialised types, like MyTime, because we can restrict, control, and specialise the operations that are possible. Object-oriented programming is particularly popular because it gives us a good way to bundle methods and specialised data into a new type. (We call such a type an abstract data type.)
Both approaches are powerful problem-solving techniques. Often it may help to try to think about the problem from both points of view --- "What would happen if I tried to reduce everything to very few primitive types?", versus "What would happen if this thing had its own specialised type?"
Glossary
- functional programming style
- A style of program design in which the majority of functions are pure.
- generalisation
- A problem-solving technique where a concrete problem gets generalised into a more abstract one that is easier to solve
- modifier
- A function or method that changes one or more of the objects it receives as parameters. Most modifier functions are void (do not return a value).
- normalized
- Data is said to be normalized if it fits into some reduced range or set of rules. We usually normalize our angles to values in the range [0..360[. We normalize minutes and seconds to be values in the range [0..60[. And we'd be surprised if the local store advertised its cold drinks at "One dollar, two hundred and fifty cents".
- pure function
- A function that does not modify any of the objects it receives as parameters. Most pure functions are not void but return a value.
- specialisation
- A problem-solving technique where a more abstract problem gets specialised into a more concrete one that is easier to solve
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Overloading and Polymorphism
Source: this section is heavily based on the second half of Chapter 21 of [ThinkCS] though adapted to better fit with the contents, terminology and notations of this particular course.
In the previous chapter we introduced a new class MyTime representing time objects in hours, minutes and seconds with methods like __init__, __str__, increment and to_seconds. For easy reference, we repeat the implementation of this class so far here below:
class MyTime: def __init__(self, hrs=0, mins=0, secs=0): """ Create a new MyTime object initialised to hrs, mins, secs. @pre: hrs, mins, secs are positive integers; if not supplied a default value of 0 is used @post: the attributes hours, minutes and seconds of this MyTime object have been initialised to hrs, mins, secs (or 0 if no values were supplied) In case the values of mins and secs are outside the range 0-59, the resulting MyTime object will be normalised, so that they are in this range """ # Calculate the total number of seconds to represent totalsecs = hrs*3600 + mins*60 + secs self.hours = totalsecs // 3600 # Split in h, m, s leftoversecs = totalsecs % 3600 self.minutes = leftoversecs // 60 self.seconds = leftoversecs % 60 def __str__(self) : """ @pre: - @post: returns a string representation of this MyTime object in the format "hh:mm:ss" """ return "{0:2}:{1:2}:{2:2}".format(self.hours, self.minutes, self.seconds) def increment(self, secs): """ @pre: t is an instance of MyTime; secs is a positive integer @post: the seconds attribute of t is modified by adding secs; if necessary t gets normalized so that neither the amount of seconds in t nor the amount of minutes in t becomes > 60; nothing is returned """ self.__init__(self.hours,self.minutes,self.seconds+secs) def to_seconds(self): """ @pre: - @post: returns the total number of seconds represented by this instance of MyTime """ return self.hours * 3600 + self.minutes * 60 + self.seconds
Binary operations
We will now add a few more interesting methods to this class. Let us start by an after function which compares two times, and tells us whether the first time is strictly after the second, e.g.
>>> t1 = MyTime(10, 55, 12) >>> t2 = MyTime(10, 48, 22) >>> t1.after(t2) # Is t1 after t2? True
This is slightly more complicated because it operates on two MyTime objects, not just one. But we'd prefer to write it as a method anyway, in this case, a method on the first argument. We can then invoke this method on one object and pass the other as an argument:
if current_time.after(done_time): print("The bread will be done before it starts!")
We can almost read the invocation like English: If the current time is after the done time, then...
To implement this method, we can again use our "Aha!" insight of the previous chapter and reduce both times to seconds, which yields a very compact method definition:
class MyTime: # Previous method definitions here... def after(self, other): """ @pre: other is an instance of MyTime @post: returns True if this MyTime instance (self) is strictly greater than other; returns False otherwise """ return self.to_seconds() > other.to_seconds()
This is a great way to code this: if we want to tell if the first time is after the second time, turn them both into integers and compare the integers.
Operator overloading
Some languages, including Python, make it possible to have different meanings for the same operator when applied to different types. For example, + in Python means quite different things for integers and for strings. This feature is called operator overloading.
It is especially useful when programmers can also overload the operators for their own user-defined types.
For example, to override the addition operator + for MyTime objects, we can provide a magic method named __add__:
class MyTime: # Previously defined methods here... def __add__(self, other): """ @pre: other is an instance of class MyTinme @post: a new MyTime object is returned of which the total time in seconds is the sum of the total time in seconds of t1 and t2 """ secs = self.to_seconds() + other.to_seconds() return MyTime(0, 0, secs)
As usual, the first parameter self is the MyTime object on which the method is invoked. The second parameter is conveniently named other to distinguish it from self. To add two MyTime objects, we create and return a new MyTime object that contains their sum in seconds. (Remember from the previous chapter that the __init__ method normalises MyTime objects by converting their value in seconds to hours, minutes and seconds.)
Now, when we apply the + operator to MyTime objects, Python magically invokes the __add__ method that we have written:
>>> t1 = MyTime(1, 15, 42) >>> t2 = MyTime(3, 50, 30) >>> t3 = t1 + t2 >>> print(t3) 5: 6:12
The expression t1 + t2 is equivalent to t1.__add__(t2), but obviously more elegant. As an exercise, add a method __sub__(self, other) that overloads the subtraction operator -, and try it out.
For the next couple of exercises we'll go back to the Point class defined when we first introduced objects (in chapter Classes and Objects – the Basics), and overload some of its operators. Firstly, adding two points adds their respective (x, y) coordinates:
class Point: # Previously defined methods here... def __add__(self, other): """ @pre: other is an instance of class Point @post: retuns a new instance of class Point of which the x-coordinate (resp. y-coordinate) is the sum of the x-coordinate (resp. y-coordinate) of self and other """ return Point(self.x + other.x, self.y + other.y)
>>> p = Point(3, 4) >>> q = Point(5, 7) >>> r = p + q # equivalent to r = p.__add__(q) >>> print(r) (8, 11)
There are several ways to override the behaviour of the multiplication operator *: by defining a magic method named __mul__, or __rmul__, or both.
If the left operand of * is a Point, Python invokes __mul__, which assumes that the other operand is also a Point. In this case we compute the dot product of the two Points, defined according to the rules of linear algebra:
def __mul__(self, other): """ @pre: other is an instance of class Point @post: returns the dot product of the points contained in self and other, in other words the sum of the product of their respective x- and y-coordinates """ return self.x * other.x + self.y * other.y
If the left operand of * is a primitive type and the right operand is a Point, Python invokes __rmul__, which performs scalar multiplication:
def __rmul__(self, other): """ @pre: other is a number @post: returns the scalar multiplication of the Point object contained in self with the number contained in other; in other words a new Point object of which the x- and y-coordinates are those of self, multiplied by other """ return Point(other * self.x, other * self.y)
The result is a new Point whose coordinates are a multiple of the original coordinates. If other is a type that cannot be multiplied by a floating-point number, then __rmul__ will yield an error.
This example demonstrates both kinds of multiplication:
>>> p1 = Point(3, 4) >>> p2 = Point(5, 7) >>> print(p1 * p2) 43 >>> print(2 * p2) (10, 14) >>> print(p2 * 2)
But what happens if we try to evaluate p2 * 2? Since the first parameter is a Point, Python invokes __mul__ with 2 as the second argument. Inside __mul__, the program tries to access the x coordinate of other, which fails because an integer has no attributes:
>>> print(p2 * 2) AttributeError: 'int' object has no attribute 'x'
Unfortunately, the error message is a bit opaque. This example demonstrates some of the difficulties of object-oriented programming. Sometimes it is hard enough just to figure out what code is running.
If you wonder if we could avoid this error and make __mul__ work as well when the second argument is a number, the answer is yes:
def __mul__(self, other): """ @pre: other is an instance of class Point or a number @post: IF other is a Point object, returns the dot product of the points contained in self and other, in other words the sum of the product of their respective x- and y-coordinates IF other is a number, returns the scalar multiplication of the Point object contained in self with the number contained in other """ if type(other) is Point : return self.x * other.x + self.y * other.y if (type(other) is int) or (type(other) is float) : return other * self
Polymorphism
Most of the methods we have written so far only work for a specific type. When we create a new object, we write methods that operate on that type. But there are certain operations that we may want to apply to many types, such as the arithmetic operators + and * in the previous section. If many types support the same set of operations, we can write functions that work on any of those types.
For example, the multadd operation (which is common in linear algebra) takes three parameters; it multiplies the first two and then adds the third. We can write it in Python like this:
def multadd(x, y, z): return x * y + z
This function will work for any values of x and y that can be multiplied and for any value of z that can be added to the product.
We can invoke it with numeric values:
>>> multadd(3, 2, 1) 7
but also with Point objects:
>>> p1 = Point(3, 4) >>> p2 = Point(5, 7) >>> print(multadd (2, p1, p2)) (11, 15) >>> print(multadd (p1, p2, 1)) 44
In the first case, the Point p1 is multiplied by a scalar 2 and then added to another Point p2. In the second case, the dot product of p1 and p2 yields a numeric value, so the third parameter also has to be a numeric value.
Functions like +, * and multadd that can work with arguments of different types are called polymorphic. In object-oriented programming, polymorphism (from the Greek meaning "having multiple forms") is the characteristic of being able to assign a different meaning or usage to something in different contexts. In this case, the context that varies are the types of arguments taken by the function.
As another example, consider the function front_and_back, which prints a list twice, forward and backward:
def front_and_back(front): import copy back = copy.copy(front) back.reverse() print(str(front) + str(back))
Because the reverse method is a modifier, we first make a copy of the list before reversing it. That way, this function doesn't modify the list it gets as a parameter.
Here's an example that applies front_and_back to a list:
>>> my_list = [1, 2, 3, 4] >>> front_and_back(my_list) [1, 2, 3, 4][4, 3, 2, 1]
Since we designed this function to apply to lists, of course it is not so surprising that it works. What would be surprising is if we could apply it to a Point.
To determine whether a function can be applied to a new type, we apply Python's fundamental rule of polymorphism, called the duck typing rule: If all of the operations inside the function can be applied to the type, the function can be applied to the type. The operations in the front_and_back function include copy, reverse, and print.
Remark: Not all programming languages define polymorphism in this way. Look up 'duck typing', and see if you can figure out why it has this name.
Since copy works on any object, and we have already written a __str__ method for Point objects, all we need to add is a reverse method to the Point class, which we define as a method that swaps the values of the x and y attributes of a point:
def reverse(self): """ @pre: - @post: swaps the values of the x- and y-coordinates of this Point """ (self.x , self.y) = (self.y, self.x)
After this, we can try to pass Point objects to the front_and_back function:
>>> p = Point(3, 4) >>> front_and_back(p) (3, 4)(4, 3)
The most interesting polymorphism is often the unintentional kind, where we discover that a function which we have already written can be applied to a type for which we never planned it.
Glossary
- dot product
- An operation defined in linear algebra that multiplies two points and yields a numeric value.
- duck typing
- If all of the operations on arg inside the body of a function f(arg) can be applied to a given type, then the function can be applied to an argument arg of that type.
- operator overloading
- Extending built-in operators ( +, -, *, >, <, etc.) so that they do different things for different types of arguments. We've seen earlier how + is overloaded for numbers and strings, and here we've shown how to further overload it for user-defined types using magic methods.
- polymorphic
- A function that can operate on more than one type. Notice the subtle distinction: overloading has different functions (all with the same name) for different types, whereas a polymorphic function is a single function that can work for a range of types.
- scalar multiplication
- An operation defined in linear algebra that multiplies each of the coordinates of a Point by a numeric value.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Collections of objects
Source: this section is heavily based on Chapter 22 of [ThinkCS] though adapted to better fit with the contents, terminology and notations of this particular course.
Composition
By now, we have seen several examples of composition. One example is using a method invocation as part of an expression. Another example is the nested structure of statements: we can put an if statement within a while loop, within another if statement, and so on.
Having seen this pattern, and having learned about lists and objects, we should not be surprised to learn that we can create lists of objects. We can also create objects that contain lists (as attributes); we can create lists that contain lists; we can create objects that contain objects; and so on.
In this chapter and the next, we will look at some examples of these combinations, using Card objects as an example.
Card objects
If you are not familiar with common playing cards, now would be a good time to get a deck, or else this chapter might not make much sense. There are fifty-two cards in a deck, each of which belongs to one of four suits and one of thirteen ranks. The suits are Spades ♠︎, Hearts ♥︎, Diamonds ♦︎, and Clubs ♣︎ (in descending order in the bridge game). The ranks are Ace (1), 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, and King. Depending on the game that we are playing, the rank of Ace may be higher than King or lower than 2. The rank is sometimes called the face-value of the card.

If we want to define a new object to represent a playing card, it is obvious what its attributes should be: rank and suit. It is not as obvious what type these attributes should have. One possibility is to use strings containing words like "Spade" for suits and "Queen" for ranks. One problem with this implementation is that it would not be easy to compare cards to see which had a higher rank or suit.
An alternative is to use integers to encode the ranks and suits. By encode, we do not mean what some people think, which is to encrypt or translate into a secret code. What a computer scientist means by encode is to define a mapping between a sequence of numbers and the items he or she wants to represent. For example:
Spades <--> 3 Hearts <--> 2 Diamonds <--> 1 Clubs <--> 0
An obvious feature of this mapping is that the suits map to integers in order, so we can compare suits by comparing integers. The mapping for ranks is fairly obvious; each of the numerical ranks maps to the corresponding integer (and Ace to 1), and for face cards:
Jack <--> 11 Queen <--> 12 King <--> 13
Using such an encoding of suits and ranks as integers, the class definition for the Card type looks like this:
class Card: """ Represents a Card in a Deck of playing cards. """ def __init__(self, suit=0, rank=0): self.suit = suit self.rank = rank
As usual, we provide an initialisation method that takes an optional parameter for each attribute. (We'll explain later why we chose 0 as default value for the rank, even though 0 does not map to any existing rank.)
To create some objects, representing say the 3 of Clubs (0) and the Jack (11) of Diamonds (1), use these commands:
three_of_clubs = Card(0, 3) card1 = Card(1, 11) # Jack of Diamonds
In the first case above, the first argument, 0, represents the suit Clubs. In the second case above, the second argument, 11, represents the Jack.
Save this code for later use ...
In the next chapter we will assume that we have saved the Cards class, and the upcoming Deck class in a file called Cards.py.
Class attributes
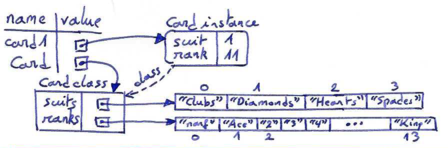
In order to print Card objects in a way that people can easily read, we want to map the integer codes back onto words. A natural way to do that is with lists of strings. We assign these lists to class attributes (or class variables) at the top of the class definition:
class Card: """ Represents a Card in a Deck of playing cards. """ suits = ["Clubs", "Diamonds", "Hearts", "Spades"] ranks = ["narf", "Ace", "2", "3", "4", "5", "6", "7", "8", "9", "10", "Jack", "Queen", "King"] def __init__(self, suit=0, rank=0): self.suit = suit self.rank = rank def __str__(self): return (Card.ranks[self.rank] + " of " + Card.suits[self.suit])
A class attribute or class variable is defined outside of any method, and it can be accessed from any of the methods in the class. To access a class attribute, you have to use the dot notation. Card.ranks refers to the class attribute ranks defined in the class Card.
Inside __str__, we can use the suits and ranks list to map the numerical values of suit and rank to strings. For example, the expression Card.suits[self.suit] means: use the instance variable suit from the object self as an index into the class attribute named suits of the class Card, and select the corresponding string.
The reason for the "narf" value (which is an acronym for "not a real face-value") as the first element in ranks is to act as a place keeper for the zero-eth element of the list, which will never be used. The only valid ranks are 1 to 13. This wasted item is not entirely necessary. We could have started at 0, by putting rank 1 at position 0 in the list, and so on, but it is much less confusing to encode the rank 2 as integer 2, 3 as 3, and so on.
With the methods we have so far, we can create and print cards:
>>> card1 = Card(1, 11) >>> print(card1) Jack of Diamonds
We can access a class variable directly via its class, like we did before:
>>> print(Card.suits[1]) Diamonds
Again, it can be useful to draw a memory diagram like the one below to clearly understand that instance variables are stored in the instance and that class variables are part of the class definition:
Alternatively, we can access a class variable via the object, for example:
>>> print(card1.suits[1]) Diamonds
What actually happens when accessing the variable suits on the object card1, is that Python will first try to find an instance variable with that name, and if that doesn't exist, following the link to the class of this instance look for a class variable with that name. This means that we could also have implemented the __str__ method above as follows (it will first look for a variable on the object itself, and if it doesn't find it there look in the class):
def __str__(self): return (self.ranks[self.rank] + " of " + self.suits[self.suit])
Personally, I prefer the former notation where it is also more explicit that we are actually accessing a class variable.
Unlike instance variables, which can have different values for each different instance of a same class, class attributes are shared by all instances of the same class. The advantage of this is that we can use any Card object to access the class attributes:
>>> card2 = Card(1, 3) >>> print(card2) 3 of Diamonds >>> print(card2.suits[1]) Diamonds
However, because every Card instance references the same class attribute, we have an aliasing situation. The disadvantage of that is that if we would modify a class attribute, this modification would affect every instance of that class. For example, if we decide that Jack of Diamonds should really be called Jack of Swirly Whales, we could do this:
>>> card1.suits[1] = "Swirly Whales" >>> print(card1) Jack of Swirly Whales
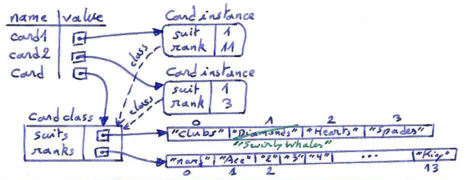
The problem is that all of the Diamonds just became Swirly Whales:
>>> print(card2) 3 of Swirly Whales
It is usually not a good idea to modify class attributes. If you do, be aware that the value will change for all instances of that class.
Comparing cards
For primitive types, there are six relational operators ( <, >, ==, <=, >=, !=) that compare values and determine when one is greater than, less than, or equal to another. If we want our own types to be comparable using the syntax of these relational operators, we need to define six corresponding magic methods in our class.
We'd like to start with a single method named cmp that captures the logic of ordering. By convention, a comparison method takes two parameters, self and other, and returns 1 if the first object is greater, -1 if the second object is greater, and 0 if they are equal to each other.
Some types are completely ordered, which means that we can compare any two elements and tell which is bigger. For example, the integers and the floating-point numbers are completely ordered. Some types are unordered, which means that there is no meaningful way to say that one element is bigger than another. For example, the fruits are unordered, which is why we cannot compare apples and oranges, and we cannot meaningfully order a collection of images, or a collection of cellphones.
Playing cards are partially ordered, which means that sometimes we can compare cards and sometimes not. For example, we know that the 3 of Clubs is higher than the 2 of Clubs, and the 3 of Diamonds is higher than the 3 of Clubs. But which is better, the 3 of Clubs or the 2 of Diamonds? One has a higher rank, but the other has a higher suit.
In order to make cards comparable, we have to decide which is more important, rank or suit. To be honest, the choice is arbitrary. For the sake of choosing, we will say that suit is more important, because a new deck of cards comes sorted with all the Clubs together, followed by all the Diamonds, and so on.
With that decided, we can write cmp:
def cmp(self, other): # Check the suits if self.suit > other.suit: return 1 if self.suit < other.suit: return -1 # Suits are the same... check ranks if self.rank > other.rank: return 1 if self.rank < other.rank: return -1 # Ranks are the same... it's a tie return 0
Note that in this ordering, Aces (1) appear lower than Deuces (2).
Now, we can define the six magic methods that do the overloading of each of the relational operators for us:
def __eq__(self, other): # equality return self.cmp(other) == 0 def __le__(self, other): # less than or equal return self.cmp(other) <= 0 def __ge__(self, other): # greater than or equal return self.cmp(other) >= 0 def __gt__(self, other): # strictly greater than return self.cmp(other) > 0 def __lt__(self, other): # strictly less than return self.cmp(other) < 0 def __ne__(self, other): # not equal return self.cmp(other) != 0
With this machinery in place, the relational operators now work as we'd like them to:
>>> card1 = Card(1, 11) >>> card2 = Card(1, 3) >>> card3 = Card(1, 11) >>> card1 < card2 False >>> card1 == card3 True
Decks
Now that we have objects to represent Cards, the next logical step is to define a class to represent a Deck. Of course, a deck is made up of cards, so each Deck object will contain a list of cards as an attribute. Some card games will need at least two different decks --- a red deck and a blue deck.

The following is a class definition for the Deck class. The initialisation method creates the attribute cards and generates the standard pack of fifty-two cards:
class Deck: def __init__(self): self.cards = [] for suit in range(4): for rank in range(1, 14): self.cards.append(Card(suit, rank))
The easiest way to populate the deck is with a nested loop. The outer loop enumerates the suits from 0 to 3. The inner loop enumerates the ranks from 1 to 13. (Remember that range(m, n) generates integers from m up to, but not including, n.) Since the outer loop iterates four times, and the inner loop iterates thirteen times, the total number of times the body is executed is 52 (13 * 4). Each iteration creates a new instance of Card with the current suit and rank, and appends that card to the cards list. (Remember that whenever the Card constructor method is invoked a new instance of class Card is created.)
With this in place, we can instantiate some decks:
red_deck = Deck() blue_deck = Deck()
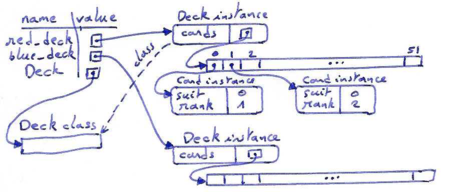
Printing the deck
As usual, when we define a new type we would like a way to print the contents of a Deck instance. One way to do so would be to implement a method to traverse the list of cards in the deck and print each Card:
class Deck: ... def print_deck(self): for card in self.cards: print(card)
Here, and from now on, the ellipsis (...) indicates that we have omitted the other methods in the class.
>>> red_deck.print_deck()
However, as we don't like chatterbox methods that call print, a better alternative to print_deck would be to write a string conversion method __str__ for the Deck class. The advantage of __str__ is that it is more flexible. Rather than just printing the contents of the object, it generates a string representation that other parts of the program can manipulate before printing, or store for later use. Here is a version of __str__ that returns a string representation of a Deck. To add a bit of flair to it, it arranges the cards in a cascade where each card is indented one space more than the previous card:
class Deck: ... def __str__(self): s,spaces = "","" for c in self.cards: s = s + spaces + str(c) + "\n" spaces += " " return s
This example demonstrates several features. First, instead of looping over the range of all cards, using an expression like for i in range(len(self.cards)), and to access each card using its index i, as in self.cards[i], instead we simply traverse self.cards and assign each card to a variable c.
Second, instead of using the print command to print the cards, we use the str function to get their print representation. Passing an object as an argument to str, i.e. str(c), is equivalent to invoking the __str__ method on the object, i.e. c.__str__() .
Thirdly, we are using the variables s and spaces as accumulators. Initially, s and spaces are empty strings. Each time through the loop, a new string is generated and concatenated to the old value of s to get the new value. Similarly, each time through the loop a single space is added to spaces to increase the indentation level. When the loop ends, s finally contains the complete string representation of the Deck, which looks like this:
>>> red_deck = Deck() >>> print(red_deck) Ace of Clubs 2 of Clubs 3 of Clubs 4 of Clubs 5 of Clubs 6 of Clubs 7 of Clubs 8 of Clubs 9 of Clubs 10 of Clubs Jack of Clubs Queen of Clubs King of Clubs Ace of Diamonds 2 of Diamonds ...
And so on. Even though the result appears on 52 lines, it is one long string that contains newlines.
Shuffling the deck
If a deck is perfectly shuffled, then any card is equally likely to appear anywhere in the deck, and any location in the deck is equally likely to contain any card.
To shuffle the deck, we will use the randrange function from the random module. With two integer arguments, a and b, randrange chooses a random integer in the range a <= x < b. Since the upper bound is strictly less than b, we can use the length of a list as the second parameter, and we are guaranteed to get a legal index in the list of cards. For example, if rng has already been instantiated as a random number source, this expression chooses the index of a random card in a deck:
rng.randrange(0, len(self.cards))
An easy way to shuffle the deck is by traversing the cards and swapping each card with a randomly chosen one. It is possible that the card will be swapped with itself, but that is fine. In fact, if we precluded that possibility, the order of the cards would be less than entirely random:
class Deck: ... def shuffle(self): import random rng = random.Random() # Create a random generator num_cards = len(self.cards) for i in range(num_cards): j = rng.randrange(i, num_cards) (self.cards[i], self.cards[j]) = (self.cards[j], self.cards[i])
>>> red_deck.shuffle() >>> print(red_deck)
Rather than assuming that there are fifty-two cards in the deck, we get the actual length of the list and store it in num_cards. This avoids having hardcoded numbers in the code, so that the algorithm is more generic and can be reused easily for other sizes of decks (such as those used for the blackjack card game).
Secondly, rather than looping over all cards, we now use a loop variable i to loop over the range of all cards, and access each card using its index i. We swap the current card at index i with one at a higher index j, chosen randomly from the cards that haven't been shuffled yet. Then we swap the current card (i) with the selected card (j) using a tuple assignment:
(self.cards[i], self.cards[j]) = (self.cards[j], self.cards[i])
While this is a good shuffling method, a random number generator object also has a shuffle method that can shuffle elements in a list, in place. So we could rewrite this function to use the one provided for us:
class Deck: ... def shuffle(self): import random rng = random.Random() # Create a random generator rng.shuffle(self.cards) # Use its shuffle method
Removing and dealing cards
Another method that would be useful for the Deck class is remove, which takes a card as a parameter, removes it and returns True, or False if the card was not in the deck (for example because it already has been removed before):
class Deck: ... def remove(self, card): if card in self.cards: self.cards.remove(card) return True else: return False
The in operator returns True if the first operand is in the second. If the first operand is an object, Python uses the object's __eq__ method to determine equality with items in the list. Since the __eq__ we provided in the Card class checks for deep equality, the remove method checks for deep equality.
To deal cards, we want to remove and return the top card. The list method pop provides a convenient way to do that:
class Deck: ... def pop(self): return self.cards.pop()
Actually, pop removes the last card in the list, so we are actually dealing from the bottom of the deck.
One more operation that we are likely to want is the Boolean function is_empty, which returns True if the deck contains no more cards:
class Deck: ... def is_empty(self): return self.cards == []
Glossary
- accumulator
- A variable used in a loop to accumulate a series of values, such as by concatenating them onto a string or adding them to a running sum.
- class attribute
- A variable that is defined inside a class definition but outside any method. Class attributes are accessible from any method in the class and are shared by all instances of the class.
- class variable
- synonym for class attribute
- encode
- To represent one type of value using another type of value by constructing a mapping between them.
- magic methods for relational operators
__eq__ (equals) overloads the == operator
__le__ (equals) overloads the <= operator
__ge__ (equals) overloads the >= operator
__lt__ (equals) overloads the < operator
__gt__ (equals) overloads the > operator
__ne__ (equals) overloads the != operator
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Inheritance
Source: this section is heavily based on Chapter 23 of [ThinkCS] though adapted to better fit with the contents, terminology and notations of this particular course.
Inheritance
The language feature most often associated with object-oriented programming is inheritance. Inheritance is the ability to define a new class that is a modified version of an existing class.
The primary advantage of this feature is that you can add new methods to a class without modifying the existing class. It is called inheritance because the new class inherits all of the methods of the existing class. Extending this metaphor, the existing class is sometimes called the parent class. The new class is called the child class or sometimes subclass.
Inheritance is a powerful feature. Some programs that would be complicated without inheritance can be written concisely and simply with it. Also, inheritance facilitates code reuse, since you can customise the behaviour of parent classes without having to modify them. In some cases, the inheritance structure reflects the natural structure of a problem, which makes the program easier to understand.
On the other hand, inheritance can sometimes make programs difficult to read. When a method is invoked, it is sometimes not clear where to find its definition, since the relevant code may be scattered among several classes. If the natural structure of a problem does not lend itself to inheritance, sometimes a more elegant solution without using inheritance is more appropriate. In general, as a computer scientist it is good to know a few different programming paradigms so that you can always choose the one that is most suited for the problem at hand.
In this chapter we will demonstrate the use of inheritance as part of a program that plays the card game [OldMaid]. One of our goals is to write the program in such a way that parts of its code could easily be reused to implement other card games. Furthermore, to implement the card game we will build upon the Card and Deck classes which we already introduced in the previous chapter.
A hand of cards
For almost any card game, we need to represent a hand of cards, i.e. the set of cards a player is holding in his hand. A Hand is similar to a Deck. Both are made up of a set of cards, and both require operations like adding and removing cards. Also, we might like the ability to shuffle both decks and hands.

But a Hand is also different from a Deck in certain ways. Depending on the game being played, we might want to perform some operations on hands that don't make sense for a deck. For example, in poker we might classify a hand (straight, flush, etc.) or compare it with another hand. In bridge, we might want to compute a score for a hand in order to make a bid.
This situation suggests the use of inheritance. If Hand is a subclass of Deck, it will have all the methods of Deck, but new methods can be added.
We add the code in this chapter to our Cards.py file from the previous chapter. In the class definition, the name of the parent class appears in parentheses:
class Hand(Deck): pass
This statement indicates that the new Hand class inherits from the existing Deck class. Such an empty child class would provide exactly the same behaviour as its super class. (In other words, instances of the child class understand exactly the same methods as instances of the super class.) This is not very useful, unless we add a few additional methods and instance variables.
We start by adding a constructor that initialises the attributes for a Hand, which are name and cards. The string name identifies this hand, probably by the name of the player that holds it. The name is an optional parameter with the empty string as default value. cards is the list of cards in the hand, initialised to the empty list:
class Hand(Deck): def __init__(self, name=""): self.cards = [] self.name = name
For just about any card game, it is necessary to add and remove cards from a hand. Removing cards is already taken care of, since Hand inherits remove from Deck. (In other words, since the super or parent class Deck already implements the method remove, any instance of class Hand will automatically understand that method as well.) But we still have to implement an add method:
class Hand(Deck): ... def add(self, card): self.cards.append(card)
Again, the ellipsis ... indicates that we have omitted other methods. The list append method adds the new card to the end of the list of cards held in the hand.
Dealing cards
Now that we have a Hand class, we want to deal cards from the Deck into hands. It is not immediately obvious whether this method should go in the Hand class or in the Deck class, but since it operates on a single deck and (possibly) several hands, it is more natural to put it in Deck.
deal should be fairly general, since different games will have different requirements. We may want to deal out the entire deck at once or add one card to each hand.
deal takes two parameters, a list (or tuple) of hands and the total number of cards to deal. If there are not enough cards in the deck, the method deals out all of the cards and stops:
class Deck: ... def deal(self, hands, num_cards=None): if num_cards==None : # if no value given for how many cards num_cards = len(self.cards) # to deal then deal all cards in deck num_hands = len(hands) for i in range(num_cards): if self.is_empty(): break # Break if out of cards card = self.pop() # Take the top card hand = hands[i % num_hands] # Whose turn is next? hand.add(card) # Add the card to the hand
The second parameter, num_cards, is optional; if no value is given for how many cards to deal, then we set the value to the size of the deck, so that all of the cards in the deck will get dealt.
The loop variable i goes from 0 to num_cards-1. Each time through the loop, a card is removed from the deck using the list method pop, which removes and returns the last item in the list.
The modulus operator (%) allows us to deal cards in a round robin (one card at a time to each hand). When i is equal to the number of hands in the list, the expression i % num_hands wraps around to the beginning of the list (index 0).
Printing a Hand
To print the contents of a hand, we can take advantage of the __str__ method inherited from Deck. For example:
>>> deck = Deck() >>> deck.shuffle() >>> hand = Hand("frank") >>> deck.deal([hand], 5) >>> print(hand) 2 of Spades 3 of Spades 4 of Spades Ace of Hearts 9 of Clubs
Although it is convenient to inherit the existing method, there is additional information in a Hand object we might want to include when we print one. To do that, we can provide a __str__ method in the Hand class that overrides the one in the Deck class:
class Hand(Deck) ... def __str__(self): s = "Hand " + self.name if self.is_empty(): s += " is empty\n" return s else: s += " contains\n" return s + Deck.__str__(self)
Initially, s is a string that identifies the hand. If the hand is empty, the program appends the words is empty and returns s.
Otherwise, the program appends the word contains and the string representation of the Deck, computed by invoking the __str__ method in the Deck class on self.
>>> deck = Deck() >>> deck.shuffle() >>> hand = Hand("frank") >>> deck.deal([hand], 5) >>> print(hand) Hand frank contains 2 of Spades 3 of Spades 4 of Spades Ace of Hearts 9 of Clubs
Method overriding and super calls
Let us analyse the previous string conversion method a bit more closely. Something very interesting is going on there! The method __str__ of the Hand class is said to override the one of the Deck class.
The word override has a very specific meaning here. It is not synonymous with the word overwrite. We do more than simply overwriting the parent class' implementation of __str__ by replacing it with a new one. In fact, the new implementation refines the old one, by making use of it, and doing a bit more. This combination of overwriting a method of the parent class, while at the same time refining it in such a way that the new implementation makes use of the old one, is called method overriding.
In the code above this happens in the expression Deck.__str__(self) inside the implementation of the method __str__(self) of the Hand class. This is an example of an explicit super call. The Hand's method __str__(self) calls __str__(self) on the super class Deck by explicitly referring to that super class.
Note that in the expression Deck.__str__(self), it may seem odd to pass self, which refers to the current Hand, to a Deck method, until you remember that a Hand is a kind of Deck. Hand objects can do everything Deck objects can, so it is legal to pass a Hand to a Deck method.
In general, it is always legal to use an instance of a subclass in place of an instance of a parent class.
An alternative way to write the __str__ method in the Hand class would be to make use of the special super() method in Python:
class Hand(Deck) ... def __str__(self): s = "Hand " + self.name if self.is_empty(): s += " is empty\n" return s else: s += " contains\n" return s + super().__str__()
The only change with respect to the previous implementation is the last line. Rather than referring to the super class Deck explicitly, the super() method allows us to refer to that super class implicitly. Also note that we don't have to pass self as an argument anymore when making such a super call.
The main advantage of using super() is that it allows us to avoid referring to the super class explicitly by name. This is considered as good object-oriented programming style. Most other object-oriented programming languages have a similar super keyword to allow methods overriding a method in their parent class, to call and extend that parent method.
The CardGame class
The CardGame class takes care of some basic chores common to all games, such as creating the deck and shuffling it:
class CardGame: def __init__(self): self.deck = Deck() self.deck.shuffle()
This is the first case we have seen where the initialisation method performs a significant computation, beyond initialising attributes. For more complex classes, like this one, that will often be the case. (As a side note, the initialisation method of a subclass will also often refine the initialisation method of its parent class using a super call. That is not the case here since CardGame is not a subclass.)
To implement specific games, we can inherit from CardGame and add features for the new game. As an example, we'll write a simulation for the [OldMaid] card game.
The object of Old Maid is to get rid, as soon as possible, of all the cards in your hand. You do this by matching cards by rank and colour. For example, the 4 of Clubs ♣︎ matches the 4 of Spades ♠︎ since they have the same rank (4) and both suits (♣︎,♠︎) are black. The Jack of Hearts ♥︎ matches the Jack of Diamonds ♦︎ since both Jacks are of the red colour.
Before starting the game, the Queen of Clubs is removed from the deck. (Other variants of the [OldMaid] game exist where the card removed from the deck is another one, but that doesn't change the essence of the game.) As a consequence of having removed the Queen of Clubs, its corresponding card, the Queen of Spades, will never be matched during the game. The player who remains with this card, the old maid, at the end of the game, loses the game.
The 51 remaining cards are now dealt to the players in a round robin fashion. After the deal, all players can discard all matching pairs of cards they have in their hand.
When no more matches can be made, the actual play begins. In turn, each player picks a card (without looking) from his closest neighbor to the left who still has cards. If the chosen card matches a card in the player's own hand, he can discard this pair from his hand. Otherwise, the chosen card is added to the player's hand. Eventually, as the game continues, all possible matches are made, except for the Queen of Spades (for which no match exists, as the Queen of Clubs was removed from the deck before starting the game). The player who remains with the Queen of Spades in his hand loses the game. (This game is particular in the sense that it has a unique loser, not a winner.)
In our computer simulation of the game, the computer will play all hands. Unfortunately, some funny nuances of the real game are lost. In a real game, the player with the Old Maid goes to some effort to get their closest neighbor to pick that card, by displaying it a little more prominently, or perhaps failing to display it more prominently, or even failing to fail to display that card more prominently. The computer simply picks a neighbor's card at random.
OldMaidHand class
A hand for playing the Old Maid game requires some abilities beyond the general abilities of a Hand, such as the ability to remove matching cards from the hand. We will therefore define a new class, OldMaidHand, that inherits from Hand to reuse its functionality, and provides an additional method called remove_matches:
class OldMaidHand(Hand): def remove_matches(self): count = 0 original_cards = self.cards.copy() for i in range(0,len(original_cards)): card = original_cards[i] for j in range(i+1,len(original_cards)): match = original_cards[j] if match == Card(3 - card.suit, card.rank): self.cards.remove(card) self.cards.remove(match) count += 1 print("Hand {0}: {1} matches {2}".format(self.name, card, match)) break return count
We start by making a copy of the list of cards, so that we can traverse the copy while removing cards from the original. Since self.cards will be modified in the loop, we don't want to use it to control the traversal. Python (or any other programming language, for that matter) can get quite confused if it is traversing a list that is changing while being traversed!
For each card in our hand (outer loop), we iterate over all the remaining cards in our hand (inner loop) to check whether they match that card. In the inner loop, we are smart and only consider cards after the current card being compared, since all the ones before have already been compared.
We have a match if the match has the same rank and the other suit of the same color. Conveniently, the expression 3 - card.suit turns a Club ♣︎ (suit 0) into a Spade ♠︎ (suit 3) and a Diamond ♦︎ (suit 1) into a Heart ♥︎ (suit 2). You should satisfy yourself that the opposite operations also work. This clever trick works because of how we encoded suits as numbers. A clever encoding often may make certain operations surprisingly easy.
Whenever we find a match, we remove both the card and its match from our hand, and jump out of the inner loop, since no other matches for this card will be found.
The following example demonstrates how to use remove_matches:
>>> game = CardGame() >>> hand = OldMaidHand("frank") >>> game.deck.deal([hand], 13) >>> print(hand) Hand frank contains 2 of Hearts 6 of Diamonds 9 of Clubs 6 of Hearts Jack of Diamonds 7 of Diamonds 10 of Spades 7 of Clubs 3 of Hearts 7 of Hearts 3 of Spades 10 of Clubs 8 of Clubs >>> count = hand.remove_matches() Hand frank: 6 of Diamonds matches 6 of Hearts Hand frank: 7 of Diamonds matches 7 of Hearts Hand frank: 10 of Spades matches 10 of Clubs >>> print("{} matches found".format(count)) 3 matches found >>> print(hand) Hand frank contains 2 of Hearts 9 of Clubs Jack of Diamonds 7 of Clubs 3 of Hearts 3 of Spades 8 of Clubs
Notice that there is no __init__ method for the OldMaidHand class. We inherit it from Hand.
Alternative implementation
Here's an alternative and slightly more compact implementation of the remove_matches method. Which one you prefer is a matter of personal taste.
class OldMaidHand(Hand): def remove_matches(self): count = 0 original_cards = self.cards.copy() for card in original_cards: match = Card(3 - card.suit, card.rank) if match in self.cards: self.cards.remove(card) self.cards.remove(match) count += 1 print("Hand {0}: {1} matches {2}".format(self.name, card, match)) return count
OldMaidGame class
Now we can turn our attention to the game itself. OldMaidGame is a subclass of CardGame. Since __init__ is inherited from CardGame, a new OldMaidGame object already contains a new shuffled deck. OldMaidGame defines a new method called play that takes a list of player names as a parameter. Calling this play method launches the game:
OldMaidGame().play(["kim","charles","siegfried"])
The play method is defined as follows:
class OldMaidGame(CardGame): ... def play(self, names): # Remove Queen of Clubs queen_clubs = Card(0,12) self.deck.remove(queen_clubs) # Make a hand for each player self.hands = [] for name in names: self.hands.append(OldMaidHand(name)) # Deal the cards self.deck.deal(self.hands) print("---------- Cards have been dealt") self.print_hands() # Remove initial matches print("---------- Discarding matches from hands") matches = self.remove_all_matches() print("---------- Matches have been discarded") self.print_hands() # Play until all 50 cards are matched # in other words, until 25 pairs have been matched print("---------- Play begins") turn = 0 num_players = len(names) while matches < 25: matches += self.play_one_turn(turn) turn = (turn + 1) % num_players print("---------- Game is Over") self.print_hands()
Some of the steps of the game have been separated into methods. The auxiliary method print_hands is pretty straightforward:
class OldMaidGame(CardGame): ... def print_hands(self): for hand in self.hands: print(hand)
remove_all_matches traverses the list of hands and invokes remove_matches on each:
class OldMaidGame(CardGame): ... def remove_all_matches(self): count = 0 for hand in self.hands: count += hand.remove_matches() return count
count is an accumulator that adds up the number of matches in each hand. When we've gone through every hand, the total is returned (count). We need this count to stop the game after 25 matches have been found. Indeed, when the total number of matches reaches 25, we know that 50 cards have been removed from the hands, which means that only 1 card is left (the old maid) and the game is over.
The variable turn keeps track of which player's turn it is. It starts at 0 and increases by one each time; when it reaches num_players, the modulus operator wraps it back around to 0.
The method play_one_turn takes a parameter that indicates whose turn it is. The return value is the number of matches made during this turn:
class OldMaidGame(CardGame): ... def play_one_turn(self, i): print("Player" + str(i) + ":") if self.hands[i].is_empty(): return 0 neighbor = self.find_neighbor(i) picked_card = self.hands[neighbor].pop() self.hands[i].add(picked_card) print("Hand", self.hands[i].name, "picked", picked_card) count = self.hands[i].remove_matches() self.hands[i].shuffle() return count
If a player's hand is empty, that player is out of the game, so he or she does nothing and 0 matches are returned.
Otherwise, a turn consists of finding the first player on the left that has cards, taking one card from the neighbor, and checking for matches. Before returning, the cards in the hand are shuffled so that the next player's choice is random.
The method find_neighbor starts with the player to the immediate left and continues around the circle until it finds a player that still has cards:
class OldMaidGame(CardGame): ... def find_neighbor(self, i): num_hands = len(self.hands) for next in range(1,num_hands): neighbor = (i + next) % num_hands if not self.hands[neighbor].is_empty(): return neighbor
If find_neighbor ever went all the way around the circle without finding cards, it would return None and cause an error elsewhere in the program. Fortunately, we can prove that that will never happen (as long as the end of the game is detected correctly).
Putting it all together
In the appendix chapter you will find the full code of all classes we defined above, as well as a sample output of a run of the game.
Glossary
- ancestor class
- A parent class, or an ancestor of the parent class.
- child class
- A new class created by inheriting from an existing class; also called a subclass.
- inheritance
- The ability to define a new class that is a modified version of a previously defined class.
- method overriding
- When, in addition to overwriting a method higher up the hierarchy, the implementation of that new method also refines the old one, by making use of it through a super call, and doing a bit more.
- method overwriting
- When a method defined in a child class replaces the implementation of a method with the same name defined in a parent or ancestor class.
- parent class
- The class from which a child class inherits; also called a superclass
- subclass
- Another word for child class.
- superclass
- another word for parent class.
- super call
- A super call can be used to gain access to inherited methods – from a parent or ancestor class – that have been overridden in a child class. This can either be done by explicitly referring to that parent class, or implicitly by using the special super() function.
Linked lists
Source: this section is largely based on Chapter 24 of [ThinkCS] though adapted to better fit with the contents, terminology and notations of this particular course. In particular, some of the code in this chapter has been adapted to use a more object-oriented style.

Embedded references
We have seen examples of attributes that refer to other objects. For example, the CardGame class referred to a Deck object as one of its attributes. We call such objects contained in another one embedded references.
We have also seen examples of data structures, such as lists and tuples. For example, Deck objects contain a list of Card objects.
A data structure is a mechanism for grouping and organising data to make it easier to use.
In this section, we will use object-oriented programming and objects with embedded references to define our own data structure, a data structure commonly known as a linked list.
Linked lists are made up of Node objects, where each node (the last node excepted) contains a reference to the next node in the linked list. In addition, each node carries a unit of data called its cargo.
A linked list can be regarded as a recursive data structure because it has a recursive definition:
A linked list is either:
- the empty list, represented by None, or
- a node that contains a cargo object and a reference to a linked list.
Recursive data structures lend themselves to recursive methods. A recursive method is a method that invokes itself, typically on a subset of the data on which it was originally invoked. For example, a method to print a linked list could first print the cargo of the node at the head of the list, and then recursively invoke itself on the embedded linked list that node refers to.
The Node class
As always when writing a new class, we'll start with the initialisation and __str__ methods so that we can test the basic mechanism of creating and displaying the new type:
class Node: """ Represents a Node in a LinkedList data structure. """ def __init__(self, cargo=None, next=None): """ Creates a new Node object. @pre: - @post: A new Node object has been initialised. A node can contain a cargo and a reference to another node. If none of these are given, the node is initialised with empty cargo (None) and no reference (None). """ self.cargo = cargo self.next = next def __str__(self): """ @pre: - @post: Returns a print representation of the cargo contained in this Node. """ return str(self.cargo)
As usual, the parameters for the initialisation method are optional. By default, both the cargo and the link to the next node, are set to None.
The string representation of a node is just the string representation of its cargo. Since any value can be passed to the str function, we can store any value in a linked list.
To test the implementation so far, we can create a Node object and print it:
>>> node = Node("test") >>> print(node) test
To make it more interesting, we will now try to create a linked list with three nodes. First we create each of the three nodes.
>>> node1 = Node(1) >>> node2 = Node(2) >>> node3 = Node(3)
This code creates three nodes, but we don't have a linked list yet because the nodes are not linked. The memory diagram looks like this:
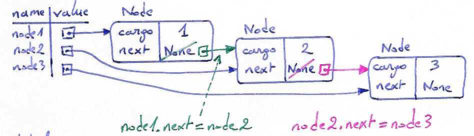
To link the nodes, we have to make the first node refer to the second one and the second one to the third:
>>> node1.next = node2 >>> node2.next = node3 >>> linkedlist = node1
The next reference of the third node remains None, which indicates that it is the end of the linked list. Now the memory diagram looks like this:

Now you know how to create nodes and link them into lists. What might be less clear at this point is why.
Linked lists as collections
Linked lists and other data structures are useful because they provide a way to assemble multiple objects into a single entity, sometimes called a collection. In our example, the first node of a linked list serves as a reference to the entire list (since from the first node, all the other nodes in the list can be reached).
To pass a linked list as a parameter, we only have to pass a reference to its first node. For example, the function print_list below takes a single node as an argument. Starting with the head of a linked list, it prints each node until it gets to the end:
def print_list(node): """ Prints the cargo of this node and of each node it is linked to. @pre: node is an instance of class Node @post: Has printed a space-separated list of the form "a b c ... ", where "a" is the string-representation of this node, "b" is the string-representation of my next node, and so on. A space is printed after each printed value. """ while node is not None: print(node, end=" ") node = node.next
To invoke this function, we pass a reference to the first node:
>>> print_list(node1) 1 2 3
Inside print_list we have a reference to the first node of the linked list. From there, to get to the next nodes, we can use the next attribute of each node. To traverse a linked list, it is common to use a loop variable like node to refer to each of the nodes in succession. This diagram shows the different values that the node variable takes on:
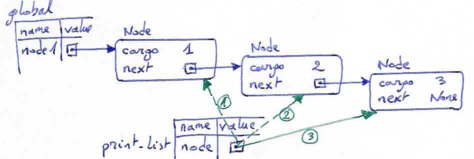
Linked lists and recursion
Since the linked list data structure is defined as a class, it would have been more natural to define the print_list function as a method on the Node class. When doing so, the method needs to be defined in a recursive way, by first printing the cargo of its head and then recursively invoking the print_list method on the next node, until no more nodes are left:
class Node: ... def print_list(self): """ Prints the cargo of this node and then recursively of each node connected to this one. @pre: The linked data structure of which this node is the head contains no loops. @post: Has printed a space-separated list of the form "a b c ... ", where "a" is the string-representation of this node, "b" is the string-representation of my next node, and so on. A space is printed after each printed value. """ print(self, end=" ") # print my head tail = self.next # go to my next node if tail is not None : # as long as the end of the list was not reached tail.print_list() # recursively print remainder of the list
To call this method, we just send it to the first node:
>>> node1.print_list() 1 2 3
In general, it is natural to express many operations on linked lists as recursive methods. The following is a recursive algorithm for printing a list backwards:
- Separate the list into two pieces: its first node (called the head); and the remainder (called the tail).
- Print the tail backward.
- Print the head.
The code which implements this algorithm looks surprisingly similar to the code of the print_list method above, the only difference being that now the head is printed after the recursive call, instead of before :
class Node: ... def print_backward(self): """ Recursively prints the cargo of each node connected to this node (in opposite order), then prints the cargo of this node as last value. @pre: The linked data structure of which this node is the head contains no loops. @post: Has printed a space-separated list of the form "... c b a", where a is my cargo (self), b is the cargo of the next node, and so on. The nodes are printed in opposite order: the last node's value is printed first. """ tail = self.next # go to my next node if tail is not None : # as long as end of list was reached tail.print_backward() # recursively print remainder backwards print(self, end = " ") # print my head
As before, to call this method, we just send it to the first node:
>>> node1.print_backward() 3 2 1
Can we prove that print_backward will always terminate? In fact, the answer is no: some (ill-formed) linked lists can make this method crash.
Infinite lists
There is nothing to prevent a node from referring back to an earlier node in the list, including itself. For example, this figure shows a list with two nodes, one of which refers to itself:
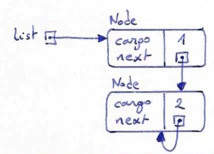
We could create such an infinite list as follows:
>>> node1 = Node(1) >>> node2 = Node(2) >>> node1.next = node2 >>> node2.next = node2
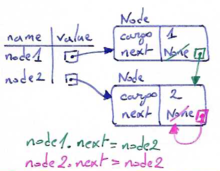
If we call either print_list or print_backward on this list, it will try to recurse infinitely, which soon leads to an error like:
RecursionError: maximum recursion depth exceeded
This sort of behaviour makes infinite lists difficult to work with. Nevertheless, they are occasionally useful. For example, we might represent a number as a list of digits and use an infinite list to represent a repeating fraction.
Regardless, it is problematic that we cannot prove that print_list and print_backward terminate. The best we can do is the hypothetical statement, "if the list contains no loops, then these methods will terminate", and use this as a precondition to be satisfied by the methods.
Ambiguity between lists and nodes
When looking at the code of the print_list or print_backward methods above, there is sometimes ambiguity between whether a reference to a node should be interpreted as a reference to a single node or rather as a reference to an entire linked list having that node as its first node.
For example, when we write print(self, end=" ") we seem to regard self as referring to a single node that is the head of this linked list, and we use the print function to print the value of its cargo.
On the other hand, when assigning self.next to a variable named tail, we seem to be regarding self.next not as a single node but rather as the entire linked list that has the next node as first node.
The fundamental ambiguity theorem describes the ambiguity that is inherent in a reference to a node of a linked list: A variable that refers to a node of a linked list might treat the node as a single object or as the first in a list of nodes.
Modifying lists
There are two ways to modify a linked list. Obviously, we can change the cargo of one of its nodes, but the more interesting operations are the ones that add, remove, or reorder nodes.
As an example, let's write a method that removes the second node in the list and returns a reference to the removed node:
class Node: ... def remove_second(self): """ @pre: The linked data structure of which this node is the first node contains no loops. @post: Does nothing if the linked list with this node as head has no second node; else removes the second node from this linked list, and returns a reference to the removed and unlinked second node. """ first = self second = self.next # do nothing if there is no second node if second is None: return # Make the first node refer to the third first.next = second.next # Separate the second node from the rest of the list second.next = None return second
We are using temporary variables first and second here to make the code more readable. Here is how to use this method:
>>> node1.print_list() 1 2 3 >>> removed = node1.remove_second() >>> removed.print_list() 2 >>> node1.print_list() 1 3
This state diagram shows the effect of the operation:
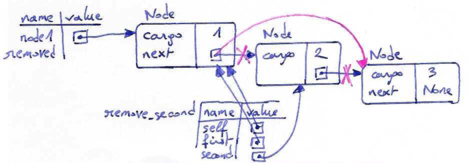
Wrappers and helpers
It is often useful to divide a list operation into two methods. For example, to print a list backward in a more conventional format [3 2 1], we can use the print_backward method to print 3 2 1 but we need a separate method to print the brackets. Let's call it print_backward_nicely:
class Node: ... def print_backward_nicely(self): """ @pre: The linked data structure of which this node is the head contains no loops. @post: Has printed a space-separated list of the form "[ ... c b a ]", where a is my cargo (self), b is the cargo of the next node, and so on. The nodes are printed in opposite order: the last node's value is printed first. A space is printed after and before the opening and closing bracket, as well as between any two elements. An empty linked is printed as "[ ]" """ print("[", end=" ") self.print_backward() print("]")
When we use this method elsewhere in the program, we invoke print_backward_nicely directly, and it invokes print_backward on our behalf. In that sense, print_backward_nicely acts as a wrapper, and it uses print_backward as a helper.
The LinkedList class
There remains a subtle problem with the way we have been implementing linked lists so far, namely that the empty list is represented in a different way (None) as a non-empty list (a collection of Node objects chained to each other). To solve this problem, we will create a new class called LinkedList. Its attributes are an integer that contains the length of the list and a reference to the first node. In case of an empty list the length attribute is 0 and the reference to the first node is None. LinkedList objects serve as handles for manipulating lists of Node objects:
class LinkedList: """ Represents a linked list datastructure. """ def __init__(self): """ Initialises a new LinkedList object. @pre: - @post: A new empty LinkedList object has been initialised. It has 0 length, contains no nodes and its head points to None. """ self.length = 0 self.head = None
Adding an element to the front of a LinkedList object can be defined straightforwardly. The method add is a method for LinkedLists that takes an item of cargo as an argument and puts it in a newly created note at the head of the list. This works regardless of whether the list is initially empty or not.
class LinkedList: ... def add(self, cargo): """ Adds a new Node with given cargo to the front of this LinkedList. @pre: self is a (possibly empty) LinkedList. @post: A new Node object is created with the given cargo. This new Node is added to the front of the LinkedList. The length counter has been incremented. The head of the list now points to this new node. Nothing is returned. """ node = Node(cargo) node.next = self.head self.head = node self.length += 1
The LinkedList class also provides a natural place to put wrapper functions like our method print_backward_nicely, which we can make a method of the LinkedList class:
class LinkedList: ... def print_backward(self): """ Prints the contents of this LinkedList and its nodes, back to front. @pre: self is a (possibly empty) LinkedList @post: Has printed a space-separated list of the form "[ ... c b a ]", where "a", "b", "c", ... are the string representation of each of the LinkedList's nodes. The nodes are printed in opposite order: the last nodes' value are printed first. A space is printed after and before the opening and closing bracket, as well as between any two elements. An empty linked is printed as "[ ]" """ print("[", end=" ") if self.head is not None: self.head.print_backward() print("]")
We renamed print_backward_nicely to print_backward when defining it on the LinkedList class. This is a nice example of polymorphism. There are now two methods named print_backward: the original one defined on the Node class (the helper); and the new one on the LinkedList class (the wrapper). When the wrapper method invokes self.head.print_backward(), it is invoking the helper method, because self.head is a Node object. To avoid calling this helper method on an empty list (when self.head is None), we added a condition to check for that situation.
In a similar way we can define a print method on the LinkedList class, to print the entire list nicely with surrounding brackets. This method is implemented in a very similar way to the print_backward method, using the print_list method on the Node class as a helper method.
class LinkedList: ... def print(self): """ Prints the contents of this LinkedList and its nodes. @pre: self is a (possibly empty) LinkedList @post: Has printed a space-separated list of the form "[ a b c ... ]", where "a", "b", "c", ... are the string representation of each of the linked list's nodes. A space is printed after and before the opening and closing bracket, as well as between any two elements. An empty linked is printed as "[ ]" """ print("[", end=" ") if self.head is not None: self.head.print_list() print("]")
The code below illustrates how to create and print linked lists using this new LinkedList class.
>>> l = LinkedList() >>> print(l.length) 0 >>> l.print() [ ] >>> l.add(3) >>> l.add(2) >>> l.add(1) >>> l.print() [ 1 2 3 ] >>> l.print_backward() [ 3 2 1 ]
The full code of this LinkedList class and its corresponding Node class are provided in an appendix. As opposed to the code above, in this appendix we also hid the attributes and provided some accessor and mutator methods to access and modify these attributes.
Other useful methods can be added to this LinkedList class, such as a method to remove the first element of a list. We leave this as an exercise to the reader.
Invariants
Some lists are well formed; others are not. For example, if a list contains a loop, it will cause many of our methods to crash, so we might want to require that lists contain no loops. Another requirement is that the length value in the LinkedList object should be equal to the actual number of nodes in the list.
Requirements like these are called invariants because, ideally, they should be true of every object all the time. Specifying invariants for objects is a useful programming practice because it makes it easier to prove the correctness of code, check the integrity of data structures, and detect errors.
One thing that is sometimes confusing about invariants is that there are times when they are violated. For example, in the middle of add, after we have added the node but before we have incremented length, the invariant is violated. This kind of violation is acceptable; in fact, it is often impossible to modify an object without violating an invariant for at least a little while. Normally, we require that every method that violates an invariant must restore the invariant.
If there is any significant stretch of code in which the invariant is violated, it is important for the comments to make that clear, so that no operations are performed that depend on the invariant.
Glossary
- cargo
- An item of data contained in a node. (The data carried by the node.)
- collection
- A collection is a data structure that assembles multiple objects into a single entity.
- data structure
- A mechanism for grouping and organising data to make it easier to use.
- embedded reference
- A reference to another object stored in an attribute of an object.
- fundamental ambiguity theorem
- A reference to a list node can be treated as a single object or as the first in a list of nodes.
- helper
- A method that is not invoked directly by a caller but is used by another method to perform part of an operation. Also called auxiliary method.
- invariant
- An assertion that should be true of an object at all times (except perhaps while the object is being modified).
- link
- An embedded reference used to link one object to another.
- linked list
- A data structure that implements a collection of elements using a sequence of linked nodes.
- node
- An element of a linked list, usually implemented as an object that carries a unit of data (its cargo) and that contains an embedded reference (a link) to another object of the same type.
- precondition
- An assertion that must be true in order for a method to work correctly.
- recursive data structure
- A recursive data structure, such as a linked list, is a data structure that can be defined in terms of itself. For example, we can say that a linked list is either the empty list, or a node that carries a cargo and a link to a linked list, containing the remaining data.
- recursive method
- A recursive method is a method that invokes itself, typically on a subset of the data on which it was originally invoked.
- singleton
- A linked list with a single node.
- wrapper
- A method that acts as a middleman between a caller and a helper method, often making the method easier or less error-prone to invoke.
References
| [ThinkCS] | How To Think Like a Computer Scientist --- Learning with Python 3 |
Appendix - Code of phone example
PhoneNumber class
class PhoneNumber : def __init__(self,c,z,pr,po) : self.country = c self.zone = z self.prefix = pr self.postfix = po def call(self) : print("Calling number " + str(self)) def __str__(self): return "+" + self.country + "(0)" + self.zone \ + "/" + self.prefix + self.postfix
Creating and using PhoneNumber objects
>>> number_kim = PhoneNumber("32","10","4","79111") >>> print(number_kim) +32(0)10/479111 >>> number_kim = PhoneNumber("32","10","4","79111") >>> print(number_kim) +32(0)10/479111 >>> number_kim.call() Calling number +32(0)10/479111
NokiaPhone class
class NokiaPhone : def __init__(self,s,p,t,n) : self.marque = "Nokia" self.serie = s self.poids = p self.taille = t self.numero = n def print_type(self) : print(self.marque + " " + str(self.serie)) def print_specs(self) : self.print_type() print("Poids: " + str(self.poids) + " g") print("Taille: " + self.taille + " mm") def print(self) : self.print_specs() print(self.numero) def __eq__(self, other) : return (self.marque == other.marque) \ and (self.serie == other.serie) \ and (self.poids == other.poids) \ and (self.taille == other.taille) def __str__(self) : return self.marque + " " + str(self.serie) + "\n" \ + "Poids: " + str(self.poids) + " g" + "\n" \ + "Taille: " + self.taille + " mm" + "\n"
Creating and using NokiaPhone objects
>>> phone_kim = NokiaPhone(5110,170,"132x48x31",number_kim) >>> phone_kim.print() Nokia 5110 Poids: 170 g Taille: 132x48x31 mm +32(0)10/479111 >>> phone_kim.print_specs() Nokia 5110 Poids: 170 g Taille: 132x48x31 mm >>> phone_kim.print_type() Nokia 5110 >>> print(phone_kim) Nokia 5110 Poids: 170 g Taille: 132x48x31 mm
Attention : phone_kim.print() ≠ print(phone_kim) ! Pourquoi ?
>>> number_charles = PhoneNumber("32","10","4","79222") >>> nokia_charles = NokiaPhone(7.1,160,"150x71x8",number_charles) >>> print(nokia_charles) Nokia 7.1 Poids: 160 g Taille: 150x71x8 mm >>> number_siegfried = PhoneNumber("32","10","4","79333") >>> nokia_siegfried = NokiaPhone(5110,170,"132x48x31",number_siegfried) >>> nokia_siegfried.print_specs() Nokia 5110 Poids: 170 g Taille: 132x48x31 mm >>> phone_charles = phone_kim >>> phone_charles.marque = "Alcatel" >>> phone_charles = None >>> print(phone_kim) Alcatel 5110 Poids: 170 g Taille: 132x48x31 mm >>> nokia_kim = NokiaPhone(5110,170,"132x48x31",number_kim) >>> nokia_siegfried = NokiaPhone(5110,170,"132x48x31",number_siegfried) >>> print(nokia_kim == nokia_siegfried) # appelera la méthode magique __eq__ True >>> print(nokia_kim is nokia_siegfried) # appelera la méthode magique __eq__ False >>> import copy >>> nokia_siegfried = copy.copy(nokia_kim) >>> nokia_kim.poids = 200 >>> print(nokia_kim) Nokia 5110 Poids: 200 g Taille: 132x48x31 mm >>> print(nokia_siegfried) Nokia 5110 Poids: 170 g Taille: 132x48x31 mm >>> kim_phone = NokiaPhone(5110,170,"132x48x31",number_kim) >>> siegfried_phone = copy.copy(kim_phone) >>> charles_phone = copy.deepcopy(kim_phone) >>> number_kim.postfix = "79000" >>> kim_phone.print() Nokia 5110 Poids: 170 g Taille: 132x48x31 mm +32(0)10/479000 >>> siegfried_phone.print() Nokia 5110 Poids: 170 g Taille: 132x48x31 mm +32(0)10/479000 >>> charles_phone.print() Nokia 5110 Poids: 170 g Taille: 132x48x31 mm +32(0)10/479111
Attention : le numéro de téléphone de Charles n'a pas changé (deep copy) mais le numéro de Siegried a changé (shallow copy).
Appendix - Worked out example: accounts
Classes and objects
First let us create a class representing bank accounts ("comptes en banque"):
class Compte : def __init__(self, titulaire) : self.titulaire = titulaire self.solde = 0
Now let us create an object of this class, representing someone's bank account:
>>> a = Compte("kim") >>> print(a.titulaire) kim >>> print(a.solde) 0 >>> a.solde = 10 >>> print(a.solde) 10 >>> a.solde += 1000 >>> print(a.solde) 1010
Hiding instance variables
Of course, we don't like it too much that our bank account details are so easily accessible from the outside. So let us try to hide the attributes:
class Compte : def __init__(self, titulaire) : self.__titulaire = titulaire self.__solde = 0
As you can see, you cannot easily access the instance attributes of an object of this class, such as an account's balance, anymore:
>>> a = Compte("kim") >>> a.__titulaire AttributeError: 'Compte' object has no attribute 'titulaire' >>> a.__solde AttributeError: 'Compte' object has no attribute '__solde'
Accessor methods
But oh, wait a minute, we need to be able to at least get access to it from the inside, so we need accessor methods that allow us to access these values, and while we are at it let's add a method to be able to print the account too:
class Compte : # initialiser def __init__(self, titulaire): self.__titulaire = titulaire self.__solde = 0 # accessor def titulaire(self): return self.__titulaire # accessor def solde(self): return self.__solde # print representation def __str__(self) : return "Compte de {} : solde = {}".format(self.titulaire(),self.solde())
Remember that when we define a method we write def solde(self): and shouldn't forget the self parameter. But when we call a method on self (or on another object) we write `self.solde() without the self-parameter and Python will implicitly bind the self-parameter to the receiver object.
If you don't know or don't remember how the format() method works on strings, look it up, it's not so crucial for this example; we could easily have written the __str__ method without it, but it leads to more compact code.
Also note how we use the accessors methods titulaire() and solde() in the __str__ method as well. This makes it easier to change the internal variable if we want to.
>>> a = Compte("kim") >>> print(a) Compte de kim : solde = 0 >>> print(a.titulaire()) kim
Mutator methods
Objects carry their own state and can provide their own methods to manipulate that state. We will now add two such mutator methods (they are called like that since they mutate the state of the object); one for redrawing money from the account, and another to deposit money on the account:
class Compte : # initialiser def __init__(self, titulaire): self.__titulaire = titulaire self.__solde = 0 # accessor def titulaire(self): return self.__titulaire # accessor def solde(self): return self.__solde # string representation def __str__(self) : return "Compte de {} : solde = {}".format(self.titulaire(),self.solde()) # *** No modifications above! Only the methods below were added... *** # mutator def deposer(self, somme): self.__solde += somme return self.solde() # mutator def retirer(self, somme): if self.solde() >= somme : self.__solde -= somme return self.solde() else : return "Solde insuffisant"
Now we can add or remove money from an account with the newly added methods:
>>> compte_charles = Compte("Charles") >>> print(compte_charles) Compte de Charles : solde = 0 >>> print(compte_charles.deposer(100)) 100 >>> print(compte_charles.retirer(90)) 10 >>> print(compte_charles.retirer(50)) Solde insuffisant >>> print(compte_charles.titulaire()) Charles
Class variables
While an object's instance variables carry the state of the object that is specific to each particular instance, sometimes it is also useful to have a state that is shared by all the objects of a same class. For example, all account objects may share the same interest rate. Such shared state common to all instances of a same class can be declared in a class variable, or class attribute, defined within the class:
class Compte : # class variable taux_interet = 0.02 def __init__(self, titulaire): self.__titulaire = titulaire self.__solde = 0 def titulaire(self): return self.__titulaire def solde(self): return self.__solde # We also modify the print representation to show the interest rate def __str__(self) : return "Compte de {0} : solde = {1:4.2f} \ntaux d'intérêt = {2}".format(self.titulaire(),self.solde(),self.taux_interet) def deposer(self, somme): self.__solde += somme return self.solde() def retirer(self, somme): if self.solde() >= somme : self.__solde -= somme return self.solde() else : return "Solde insuffisant"
Two different instances of this class share the same value for the class variable, but their instance variables may vary:
>>> compte_kim = Compte("Kim") >>> print(compte_kim) Compte de Kim : solde = 0.00 taux d'intérêt = 0.02 >>> compte_siegfried = Compte("Siegfried") >>> print(compte_siegfried) Compte de Siegfried : solde = 0.00 taux d'intérêt = 0.02
Changing the state of the class variable changes it for all instances of that class:
>>> Compte.taux_interet = 0.04 >>> print(compte_kim) Compte de Kim : solde = 0.00 taux d'intérêt = 0.04 >>> print(compte_siegfried) Compte de Siegfried : solde = 0.00 taux d'intérêt = 0.04
Shadowing
Attention! It is possible for an instance variable to have the same name as a class variable. Here, we add a new instance variable to an object that will shadow the value of the class variable.
>>> compte_kim.taux_interet = 0.03
Asking the object for that variable will now return the value of the newly assigned instance variable:
>>> print(compte_kim.taux_interet) 0.03
Even though the class variable still exists with its old value: newly assigned instance variable:
>>> print(Compte.taux_interet) 0.04
Asking other objects of this class for the value of that variable will still return the value of that class variable (in these other objects, the class variable wasn't shadowed by an instance variable.
>>> print(compte_siegfried.taux_interet) 0.04
Hiding class variables and class methods
Now that we have seen how to create a class variable, we can ask ourselves the question whether there is also a way to hide a class variable so that we cannot change it from the outside?
The answer is yes: add an __ to the name, just like we did with the instance variables. But then we also need to add an accessor and a mutator method if we want to read or write the class variable externally.
These need to be declared as class methods. Class methods are methods that should be invoked on the class, not on the instance.
class Compte : __taux_interet = 0.02 @classmethod def taux_interet(cls): return cls.__taux_interet @classmethod def set_taux_interet(cls,nouveau_taux): cls.__taux_interet = nouveau_taux def __init__(self, titulaire): self.__titulaire = titulaire self.__solde = 0 def titulaire(self): return self.__titulaire def solde(self): return self.__solde def __str__(self) : return "Compte de {0} : solde = {1:4.2f} \ntaux d'intérêt = {2}".format(self.titulaire(),self.solde(),self.taux_interet()) def deposer(self, somme): self.__solde += somme return self.solde() def retirer(self, somme): if self.solde() >= somme : self.__solde -= somme return self.solde() else : return "Solde insuffisant"
Note how the class methods take an extra parameter which, by convention, is named cls and that refers to the class, just like normal instance methods took an extra parameter self that refer to the receiving object.
>>> compte_kim = Compte("Kim") >>> Compte.taux_interet() 0.02
Note that, in Python, you can invoke the class method on the instance too! That may be a bit confusing, but what happens is that Python first tries to send the method to the object instance, and if it cannot find an instance method with that name it will invoke it instead as a class method on the class of that instance.
>>> compte_kim.taux_interet() 0.02
Inheritance
Now let us consider a special kind of account, a checkings account, which inherits from the general account type and adds one additional method.
Inheritance is one of the core concepts of object-oriented programming. It enables the creation of a new (refined) class from an existing one, called its parent class. The new class, called subclass or child class, inherits all attributes and methods of the existing one.
To indicate that a class inherits from a another one, put the name of the parent class in parenthesis after the class name:
class CompteCourant(Compte) : def transferer(self,compte,montant) : res = self.retirer(montant) if res != "Solde insuffisant" : compte.deposer(montant) return res
This is the complete definition of the checkings account class CompteCourant. All other methods and attributes are simply inherited from the account superclass Compte.
>>> compte_kim = CompteCourant("Kim") >>> compte_charles = CompteCourant("Charles") >>> compte_kim.deposer(100) >>> compte_kim.transferer(compte_charles,50) >>> print(compte_kim.solde()) 50 >>> print(compte_charles.solde()) 50 >>> print(compte_kim.transferer(compte_charles,60)) Solde insuffisant
Method overriding
Also we can redefine existing methods such as the method for withdrawing money that charges 0.10 Euro extra for every cash withdrawal.
class CompteCourant(Compte) : __frais_retirer = 0.10 def transferer(self,compte,montant) : res = self.retirer(montant) if res != "Solde insuffisant" : compte.deposer(montant) return res def retirer(self, somme): return Compte.retirer(self, somme + self.__frais_retirer)
Note how this method retirer overrides a method with the same name already defined in the superclass Compte. In fact, for its implementation, this method makes use of the method defined on that superclass, by explicitly calling the method on that class and passing self as argument. This seems to have the desired effect:
>>> compte_kim = CompteCourant("Kim") >>> print(compte_kim.deposer(1000)) 1000 >>> print(compte_kim.retirer(10)) 989.9 >>> print(compte_kim.retirer(10)) 979.8
Super call
The above implementation of the method retirer seems to work, but the explicit call to Compte.retirer could be avoided.
So why not write the method with a self-call like this?
def retirer(self, somme): return self.retirer(somme + self.__frais_retirer)
If you would try that, you would get the following error upon calling that method:
RecursionError: maximum recursion depth exceeded
The reason is that, rather than calling the method on the superclass, the method would call itself (which would recursively call itself, and so on).
However, there is a better way to call the method on the super class, by using a super call with the special method super():
class CompteCourant(Compte) : __frais_retirer = 0.10 @classmethod def frais_retirer(cls): return cls.__frais_retirer def __init__(self, titulaire,banque) : super().__init__(titulaire) self.__banque = banque def retirer(self, somme): return super().retirer(somme + self.frais_retirer()) def __str__(self) : return super().__str__() + "; banque = " + self.__banque
In fact, writing
def retirer(self, somme): return super().retirer(somme + self.frais_retirer())
is equivalent to writing
def retirer(self, somme): return Compte.retirer(self, somme + self.__frais_retirer)
but has the advantage of referring to the superclass implicitly, rather than having to refer to it explicitly.
Also note how we extended the class definition with two other super calls. One in the __init__ method to initialise an additional instance variable representing the name of the bank, and another in the __str__ method. Both of these methods are defined in terms of their corresponding methods on the superclass, by making a super call.
Here is an example that shows this new class definition at work:
>>> compte_kim = CompteCourant("Kim","ING") >>> print(compte_kim.deposer(1000)) 1000 >>> print(compte_kim.retirer(10)) 989.9 >>> print(compte_kim.retirer(10)) 979.8 >>> print(compte_kim) Compte de Kim : solde = 979.80 taux d'intérêt = 0.02; banque = ING
Appendix - Code of Card Game
Card class (full code)
class Card: suits = ["Clubs", "Diamonds", "Hearts", "Spades"] ranks = ["narf", "Ace", "2", "3", "4", "5", "6", "7", "8", "9", "10", "Jack", "Queen", "King"] def __init__(self, suit=0, rank=0): self.suit = suit self.rank = rank def __str__(self): return (self.ranks[self.rank] + " of " + self.suits[self.suit]) def cmp(self, other): # Check the suits if self.suit > other.suit: return 1 if self.suit < other.suit: return -1 # Suits are the same... check ranks if self.rank > other.rank: return 1 if self.rank < other.rank: return -1 # Ranks are the same... it's a tie return 0 def __eq__(self, other): # equality return self.cmp(other) == 0 def __le__(self, other): # less than or equal return self.cmp(other) <= 0 def __ge__(self, other): # greater than or equal return self.cmp(other) >= 0 def __gt__(self, other): # strictly greater than return self.cmp(other) > 0 def __lt__(self, other): # strictly less than return self.cmp(other) < 0 def __ne__(self, other): # not equal return self.cmp(other) != 0
Deck class (full code)
class Deck: def __init__(self): self.cards = [] for suit in range(4): for rank in range(1, 14): self.cards.append(Card(suit, rank)) def print_deck(self): for card in self.cards: print(card) def __str__(self): s,spaces = "","" for c in self.cards: s = s + spaces + str(c) + "\n" spaces += " " return s def shuffle(self): import random rng = random.Random() # Create a random generator num_cards = len(self.cards) for i in range(num_cards): j = rng.randrange(i, num_cards) (self.cards[i], self.cards[j]) = (self.cards[j], self.cards[i]) def shuffle2(self): import random rng = random.Random() # Create a random generator rng.shuffle(self.cards) # Use its shuffle method def remove(self, card): if card in self.cards: self.cards.remove(card) return True else: return False def pop(self): return self.cards.pop() def is_empty(self): return self.cards == [] def deal(self, hands, num_cards=None): if num_cards==None : # if no default value for how many cards num_cards = len(self.cards) # to deal then deal all cards in deck num_hands = len(hands) for i in range(num_cards): if self.is_empty(): break # Break if out of cards card = self.pop() # Take the top card hand = hands[i % num_hands] # Whose turn is next? hand.add(card) # Add the card to the hand
CardGame class (full code)
class CardGame: def __init__(self): self.deck = Deck() self.deck.shuffle()
Hand class (full code)
class Hand(Deck): def __init__(self, name=""): self.cards = [] self.name = name def __str__(self): s = "Hand " + self.name if self.is_empty(): s += " is empty\n" return s else: s += " contains\n" return s + super().__str__() # super call by making use of the super() function (preferred) def add(self, card): self.cards.append(card) return self
OldMaidHand class (full code)
class OldMaidHand(Hand): def remove_matches(self): count = 0 # counts number of matches that have been removed original_cards = self.cards.copy() # makes a copy of the original set of cards in your hand for card in original_cards: # iterate over all cards in your hand match = Card(3 - card.suit, card.rank) if match in self.cards: # if the matching card is in your hand self.cards.remove(card) # remove the card from your hand self.cards.remove(match) # remove the match from your hand count += 1 # add one to the count of matches that have been removed print("Hand {0}: {1} matches {2}".format(self.name, card, match)) return count # return number of matches that have been removed
OldMaidGame class (full code)
class OldMaidGame(CardGame): def play(self, names): # Remove Queen of Clubs queen_clubs = Card(0,12) self.deck.remove(queen_clubs) # Make a hand for each player self.hands = [] for name in names: self.hands.append(OldMaidHand(name)) # Deal the cards self.deck.deal(self.hands) print("---------- Cards have been dealt") self.print_hands() # Remove initial matches print("---------- Discarding matches from hands") matches = self.remove_all_matches() print("---------- Matches have been discarded") self.print_hands() # Play until all 50 cards are matched # in other words, until 25 pairs have been matched print("---------- Play begins") turn = 0 num_players = len(names) while matches < 25: matches += self.play_one_turn(turn) turn = (turn + 1) % num_players print("---------- Game is Over") self.print_hands() def print_hands(self): for hand in self.hands: print(hand) def remove_all_matches(self): count = 0 for hand in self.hands: count += hand.remove_matches() return count def play_one_turn(self, i): print("Player" + str(i) + ":") if self.hands[i].is_empty(): return 0 neighbor = self.find_neighbor(i) picked_card = self.hands[neighbor].pop() self.hands[i].add(picked_card) print("Hand", self.hands[i].name, "picked", picked_card) count = self.hands[i].remove_matches() self.hands[i].shuffle() return count def find_neighbor(self, i): num_hands = len(self.hands) for next in range(1,num_hands): neighbor = (i + next) % num_hands if not self.hands[neighbor].is_empty(): return neighbor
Sample output of a run of the game
>>> OldMaidGame().play(["kim","charles","siegfried"])
---------- Cards have been dealt Hand kim contains 5 of Diamonds 10 of Diamonds Ace of Clubs Ace of Spades Jack of Hearts 4 of Clubs 3 of Clubs King of Diamonds 4 of Diamonds 10 of Clubs Ace of Hearts 5 of Hearts Queen of Diamonds Jack of Spades Jack of Diamonds 5 of Clubs 9 of Clubs Hand charles contains 5 of Spades 6 of Clubs Queen of Spades 8 of Spades 2 of Clubs 6 of Spades 9 of Hearts 8 of Hearts 10 of Hearts 9 of Diamonds 7 of Hearts 10 of Spades 9 of Spades 3 of Diamonds Jack of Clubs 7 of Spades 3 of Hearts Hand siegfried contains 7 of Clubs 6 of Diamonds 3 of Spades King of Hearts 2 of Spades 2 of Diamonds 7 of Diamonds 2 of Hearts 4 of Hearts King of Clubs 4 of Spades 8 of Clubs King of Spades 8 of Diamonds Queen of Hearts 6 of Hearts Ace of Diamonds ---------- Discarding matches from hands Hand kim: 5 of Diamonds matches 5 of Hearts Hand kim: Ace of Clubs matches Ace of Spades Hand kim: Jack of Hearts matches Jack of Diamonds Hand charles: 6 of Clubs matches 6 of Spades Hand charles: 9 of Hearts matches 9 of Diamonds Hand charles: 3 of Diamonds matches 3 of Hearts Hand siegfried: 6 of Diamonds matches 6 of Hearts Hand siegfried: 2 of Diamonds matches 2 of Hearts Hand siegfried: King of Clubs matches King of Spades ---------- Matches have been discarded Hand kim contains 10 of Diamonds 4 of Clubs 3 of Clubs King of Diamonds 4 of Diamonds 10 of Clubs Ace of Hearts Queen of Diamonds Jack of Spades 5 of Clubs 9 of Clubs Hand charles contains 5 of Spades Queen of Spades 8 of Spades 2 of Clubs 8 of Hearts 10 of Hearts 7 of Hearts 10 of Spades 9 of Spades Jack of Clubs 7 of Spades Hand siegfried contains 7 of Clubs 3 of Spades King of Hearts 2 of Spades 7 of Diamonds 4 of Hearts 4 of Spades 8 of Clubs 8 of Diamonds Queen of Hearts Ace of Diamonds ---------- Play begins Player0: Hand kim picked 7 of Spades Player1: Hand charles picked Ace of Diamonds Player2: Hand siegfried picked 7 of Spades Hand siegfried: 7 of Clubs matches 7 of Spades Player0: Hand kim picked 9 of Spades Hand kim: 9 of Clubs matches 9 of Spades Player1: Hand charles picked 8 of Clubs Hand charles: 8 of Spades matches 8 of Clubs Player2: Hand siegfried picked Jack of Spades Player0: Hand kim picked Jack of Clubs Player1: Hand charles picked 3 of Spades Player2: Hand siegfried picked Ace of Hearts Player0: Hand kim picked 10 of Hearts Hand kim: 10 of Diamonds matches 10 of Hearts Player1: Hand charles picked Queen of Hearts Player2: Hand siegfried picked 4 of Diamonds Hand siegfried: 4 of Hearts matches 4 of Diamonds Player0: Hand kim picked 3 of Spades Hand kim: 3 of Clubs matches 3 of Spades Player1: Hand charles picked King of Hearts Player2: Hand siegfried picked 4 of Clubs Hand siegfried: 4 of Spades matches 4 of Clubs Player0: Hand kim picked King of Hearts Hand kim: King of Diamonds matches King of Hearts Player1: Hand charles picked Jack of Spades Player2: Hand siegfried picked 5 of Clubs Player0: Hand kim picked 7 of Hearts Player1: Hand charles picked Ace of Hearts Hand charles: Ace of Diamonds matches Ace of Hearts Player2: Hand siegfried picked Queen of Diamonds Player0: Hand kim picked 8 of Hearts Player1: Hand charles picked 5 of Clubs Hand charles: 5 of Spades matches 5 of Clubs Player2: Hand siegfried picked Jack of Clubs Player0: Hand kim picked Queen of Spades Player1: Hand charles picked 2 of Spades Hand charles: 2 of Clubs matches 2 of Spades Player2: Hand siegfried picked Queen of Spades Player0: Hand kim picked Queen of Hearts Player1: Hand charles picked Queen of Spades Player2: Hand siegfried picked 8 of Hearts Hand siegfried: 8 of Diamonds matches 8 of Hearts Player0: Hand kim picked Queen of Spades Player1: Hand charles picked Jack of Clubs Hand charles: Jack of Spades matches Jack of Clubs Player2: Hand siegfried picked Queen of Hearts Hand siegfried: Queen of Diamonds matches Queen of Hearts Player0: Hand kim picked 10 of Spades Hand kim: 10 of Clubs matches 10 of Spades Player1: Player2: Hand siegfried picked Queen of Spades Player0: Hand kim picked 7 of Diamonds Hand kim: 7 of Hearts matches 7 of Diamonds ---------- Game is Over Hand kim is empty Hand charles is empty Hand siegfried contains Queen of Spades
Appendix - Code of Linked List
LinkedList class
class LinkedList : """ Represents a linked list datastructure. """ def __init__(self): """ Initialises a new LinkedList object. @pre: - @post: A new empty LinkedList object has been initialised. It has 0 length, contains no nodes and its head refers to None. """ self.__length = 0 self.__head = None def size(self): """ @pre: - @post: Returns the number of nodes (possibly zero) contained in this linked list. """ return self.__length def first(self): """ @pre: - @post: Returns a reference to the head of this linked list, or None if the linked list contains no nodes. """ return self.__head def add(self, cargo): """ Adds a new Node with given cargo to the front of this LinkedList. @pre: self is a (possibly empty) LinkedList. @post: A new Node object is created with the given cargo. This new Node is added to the front of the LinkedList. The length counter has been incremented. The head of the list now points to this new node. Nothing is returned. """ node = Node(cargo,self.__head) self.__head = node self.__length += 1 def print(self): """ Prints the contents of this LinkedList and its nodes. @pre: self is a (possibly empty) LinkedList @post: Has printed a space-separated list of the form "[ a b c ... ]", where "a", "b", "c", ... are the string representation of each of the linked list's nodes. A space is printed after and before the opening and closing bracket, as well as between any two elements. An empty linked is printed as "[ ]" """ print("[", end=" ") if self.__head is not None: self.__head.print_list() print("]") def print_backward(self): """ Prints the contents of this LinkedList and its nodes, back to front. @pre: self is a (possibly empty) LinkedList @post: Has printed a space-separated list of the form "[ ... c b a ]", where "a", "b", "c", ... are the string representation of each of the LinkedList's nodes. The nodes are printed in opposite order: the last nodes' value are printed first. A space is printed after and before the opening and closing bracket, as well as between any two elements. An empty linked is printed as "[ ]" """ print("[", end=" ") if self.__head is not None: self.__head.print_backward() print("]")
Node class
class Node: """ Represents a Node in a LinkedList data structure. """ def __init__(self, cargo=None, next=None): """ Creates a new Node object. @pre: - @post: A new Node object has been initialised. A node can contain a cargo and a reference to another node. If none of these are given, the node is initialised with empty cargo (None) and no reference (None). """ self.__cargo = cargo self.__next = next def value(self): """ @pre: - @post: Returns the value of the cargo contained in this node, or None if no cargo was put there. """ return self.__cargo def set_value(self,value): """ @pre: - @post: The cargo of this node has been set to value. """ self.__cargo = value def next(self): """ @pre: - @post: Returns the next node to which this node refers, or None if there is no next node. """ return self.__next def set_next(self,node): """ @pre: - @post: The next node of this node has been set to node. """ self.__next = node def __str__(self): """ @pre: self is a (possibly empty) Node object. @post: returns a print representation of the cargo contained in this Node. """ return str(self.value()) def __eq__(self,other): """ Comparator to compare two Node objects by their cargo. """ if other is not None : return self.value() == other.value() else : return False def print_list(self): """ Prints the cargo of this node and then recursively of each node connected to this one. @pre: - @post: Has printed a space-separated list of the form "a b c ... ", where "a" is the string-representation of this node, "b" is the string-representation of my next node, and so on. A space is printed after each printed value. """ print(self.value(), end=" ") # print my value tail = self.next() # go to my next node if tail is not None : # as long as the end of the list has not been reached tail.print_list() # recursively print remainder of the list def print_backward(self): """ Recursively prints the cargo of each node connected to this node (in opposite order), and then prints the cargo of this node as last value. @pre: - @post: Has printed a space-separated list of the form "... c b a", where a is my cargo (self), b is the cargo of the next node, and so on. The nodes are printed in opposite order: the last node's value is printed first. """ tail = self.next() # go to my next node if tail is not None : # as long as the end of the list has not been reached tail.print_backward() # recursively print remainder of the list backwards print(self.value(), end = " ") # print my value
Creating and using LinkedList objects
>>> l = LinkedList() >>> l.print() [ ] >>> l.print_backward() [ ] >>> print(l.size()) 0 >>> l.add(3) >>> l.add(2) >>> l.add(1) >>> l.print() [ 1 2 3 ] >>> l.print_backward() [ 3 2 1 ] >>> print(l.size()) 3